题目内容
化简：|x-1|+|x+2|+|x-4|．
考点：绝对值
专题：分类讨论
分析：分类讨论：当x≤-2时或-2＜x≤1或1＜x≤4或x＞4时，根据绝对值的意义分别去绝对值，然后合并即可．
解答：解：当x≤-2时，原式=1-x-x-2+4-x=5-3x；
当-2＜x≤1时，原式=1-x+x+2+4-x=7-x；
当1＜x≤4时，原式=x-1+x+2+4-x=x+5；
当x＞4时，原式=x-1+x-2+x-4=3x-7．
当-2＜x≤1时，原式=1-x+x+2+4-x=7-x；
当1＜x≤4时，原式=x-1+x+2+4-x=x+5；
当x＞4时，原式=x-1+x-2+x-4=3x-7．
点评：本题考查了绝对值：当a＞0，|a|=a；当a=0，|a|=0；当a＜0，|a|=-a．
练习册系列答案
相关题目
在-
，
，
4.
，
，
，这几个数中无理数有（ ）个．
| 22 |
| 7 |
| 3 | 9 |
| 25 |
| • |
| 2 |
| π |
| 2 |
| 0.4 |
| A、4 | B、3 | C、2 | D、1 |
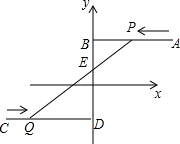如图，在平面直角坐标系中，AB∥x轴交y轴于点B，CD∥x轴交y轴于点D，且点A、点C的坐标分别为（8，3）和（-6，-2），两动点P、Q分别从点A和点C同时出发，分别沿射线AB、射线CD方向以每秒2个单位长度和每秒1个单位长度的速度匀速运动，设运动时间为t秒，线段PQ交BD于点E．
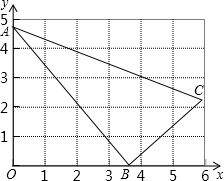如图，△ABC中，∠ABC=90°，A（0，4.8），B（3.6，0）．BC=3，