题目内容
20.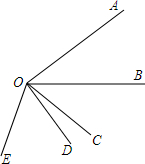 如图,∠A0B=40°,∠B0E是任意一个小于平角的角,射线0C、0D分别平分∠A0E、∠B0E,求∠C0D的度数.
如图,∠A0B=40°,∠B0E是任意一个小于平角的角,射线0C、0D分别平分∠A0E、∠B0E,求∠C0D的度数.
分析 设∠BOE=x,先求得∠AOE=40°+x,由角平分线的定义可求得∠EOC=20°+$\frac{1}{2}x$,∠EOD=$\frac{1}{2}x$,最后依据∠COD=∠EOC-∠EOD求解即可.
解答 解:设∠BOE=x.则∠AOE=∠AOB+∠BOE=40°+x.
∵射线0C、0D分别平分∠A0E、∠B0E,
∴∠EOC=20°+$\frac{1}{2}x$,∠EOD=$\frac{1}{2}x$.
∴∠DOC=∠EOC-∠EOD=20°+$\frac{1}{2}x$-$\frac{1}{2}x$=20°.
点评 本题主要考查的是角平分线的定义,表示出∠EOC和∠EOD的度数是解题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
9. 小丽想测量学校旗杆的高度,她在地面A点安置侧倾器,测得旗杆顶端C的仰角为α,侧倾器到旗杆底部的距离AD为10米,侧倾器的高度AB为1.5米,那么旗杆的高度CD为( )
小丽想测量学校旗杆的高度,她在地面A点安置侧倾器,测得旗杆顶端C的仰角为α,侧倾器到旗杆底部的距离AD为10米,侧倾器的高度AB为1.5米,那么旗杆的高度CD为( )
 小丽想测量学校旗杆的高度,她在地面A点安置侧倾器,测得旗杆顶端C的仰角为α,侧倾器到旗杆底部的距离AD为10米,侧倾器的高度AB为1.5米,那么旗杆的高度CD为( )
小丽想测量学校旗杆的高度,她在地面A点安置侧倾器,测得旗杆顶端C的仰角为α,侧倾器到旗杆底部的距离AD为10米,侧倾器的高度AB为1.5米,那么旗杆的高度CD为( )| A. | (10tanα+1.5)米 | B. | (10cosα+1.5)米 | C. | ($\frac{10}{tanα}$+1.5)米 | D. | ($\frac{10}{sinα}$+1.5)米 |
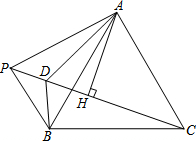 如图,P为等边△ABC外一点,AH垂直平分PC于点H,∠BAP的平分线交PC于点D.
如图,P为等边△ABC外一点,AH垂直平分PC于点H,∠BAP的平分线交PC于点D.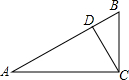 如图,△ABC中,∠ACB=90°,BC=8,AC=12,∠BCD=30°,求线段CD长.
如图,△ABC中,∠ACB=90°,BC=8,AC=12,∠BCD=30°,求线段CD长.