题目内容
8.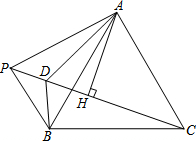 如图,P为等边△ABC外一点,AH垂直平分PC于点H,∠BAP的平分线交PC于点D.
如图,P为等边△ABC外一点,AH垂直平分PC于点H,∠BAP的平分线交PC于点D.(1)求证:DP=DB;
(2)求证:DA+DB=DC;
(3)若等边△ABC边长为$\sqrt{14}$,连接BH,当△BDH为等边三角形时,请直接写出CP的长度.
分析 (1)首先由等边三角形的性质易得AB=AC=BC,由垂直平分线的性质易得AP=AC,等量代换可得AP=AB,由SAS定理可证得△PAD≌△BAD,利用全等三角形的性质可得结论;
(2)在CP上截CQ=PD,证明△ACQ≌△APD,等量代换,证得△ADQ为等边三角形,得出结论;
(3)连接BH,延长AD交PB于E,根据PA=AB,AD是角平分线得出AE⊥PB,且平分PB,由△BDH为等边三角形,PD=BD,易得出BD=DH=BH,∠BPH=30°,解直角三角形得出DE=$\frac{1}{2}$PD,PE=$\frac{\sqrt{3}}{2}$PD,因为PD=$\frac{1}{4}$PC,AD+DB=DC,得出AD=HC=$\frac{1}{2}$PC,进而得出PE=$\frac{\sqrt{3}}{8}$PC,AE=$\frac{5}{8}$PC,然后根据勾股定理得出($\sqrt{14}$)2=($\frac{5}{8}$PC)2+($\frac{\sqrt{3}}{8}$PC)2,即可求得PC的长.
解答 (1)证明:∵△ABC为等边三角形,
∴AB=AC=BC,
∵AH垂直平分PC,
∴AP=AC,
∴AP=AB,
在△PAD与△BAD中,
$\left\{\begin{array}{l}{DA=DA}\\{∠PAD=∠BAD}\\{AP=AB}\end{array}\right.$,
∴△PAD≌△BAD(SAS),
∴DP=DB; (2)证明:如图1,在CP上截CQ=PD,
(2)证明:如图1,在CP上截CQ=PD,
∵AP=AC,
∴∠APD=∠ACQ,
在△ACQ与△APD中,
$\left\{\begin{array}{l}{AP=AC}\\{∠APD=∠ACQ}\\{PD=CQ}\end{array}\right.$,
∴△ACQ≌△APD(SAS),
∴∠PAD=∠CAQ,
∵∠PAD=BAD,
∴∠CAQ=∠BAD,
∴∠CAQ+∠BAQ=∠BAD+∠BAQ=∠DAQ=60°,
∵AD=AQ,PD=CQ=DB,
∴△ADQ为等边三角形,
∴DA=DQ,
∴DA+DB=DQ+CQ=CD; (3)解:如图2,连接BH,延长AD交PB于E,
(3)解:如图2,连接BH,延长AD交PB于E,
∵△BDH为等边三角形,
∴BD=DH=BH,∠BHD=60°,
∵DP=DB,
∴DP=DB=DH=BH,
∴BH=$\frac{1}{2}$PH,
∴△PBH是直角三角形,
∴∠BPH=30°,
∵AD是∠PAB的平分线,PA=AB,
∴AD⊥PB,
∴DE=$\frac{1}{2}$PD,PE=$\frac{\sqrt{3}}{2}$PD,
∵PD=DH=DB,PH=CH,AD+DB=DC,
∴PD=DH=$\frac{1}{4}$PC,AD=CH=$\frac{1}{2}$PC,
∴DE=$\frac{1}{8}$PC,PE=$\frac{\sqrt{3}}{8}$PC,
∴AE=AD+DE=$\frac{1}{2}$PC+$\frac{1}{8}$PC=$\frac{5}{8}$PC,
在RT△PAE中,PA2=AE2+PE2,
∴($\sqrt{14}$)2=($\frac{5}{8}$PC)2+($\frac{\sqrt{3}}{8}$PC)2,
∴PC=4$\sqrt{2}$.
点评 本题考查了全等三角形的判定和性质,线段的垂直平分线的性质,等边三角形的性质,解直角三角形,勾股定理的应用等,作出辅助线构建全等三角形和直角三角形是解题的关键.

 名校课堂系列答案
名校课堂系列答案信息一:工作时间:每天上午8:00~12:00,下午13:00~17:00,每月25天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于60件.
生产产品的件数与所用时间之间的关系如下表:
| 生产甲产品件数(件) | 生产乙产品件数(件) | 所用总时间(min) |
| 10 | 10 | 350 |
| 30 | 20 | 850 |
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分钟?
(2)若小王每月生产甲产品a件,乙产品b件,当a、b分别是多少时,小王收入最多?
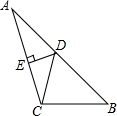 已知:△ABC中,D是AB中点,DE⊥AC于E,∠B=45°,tan∠A=$\frac{1}{2}$.
已知:△ABC中,D是AB中点,DE⊥AC于E,∠B=45°,tan∠A=$\frac{1}{2}$.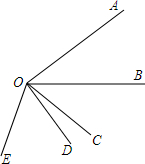 如图,∠A0B=40°,∠B0E是任意一个小于平角的角,射线0C、0D分别平分∠A0E、∠B0E,求∠C0D的度数.
如图,∠A0B=40°,∠B0E是任意一个小于平角的角,射线0C、0D分别平分∠A0E、∠B0E,求∠C0D的度数.