题目内容
12.六年级和七年级的学生参加一次乒乓球比赛,七年级的参赛人数是六年级的3倍,每两个参赛者都比赛一场且一定决出胜负.以所胜场次最多者为冠军,现知六年级学生所胜的场次数量与七年级学生所胜的场次数目相等.证明:冠军是六年级的学生.分析 设六年级有k名同学参加乒乓球比赛,则七年级有3k名同学参加比赛,再求出比赛的场数及六年级同学赢的场数,进而可得出结论.
解答 解:设六年级有k名同学参加乒乓球比赛,则七年级有3k名同学参加比赛,
∵每两个参赛者都比赛一场且一定决出胜负,
∴一共进行了2k(4k-1)场比赛,
∵六年级学生所胜的场次数量与七年级学生所胜的场次数目相等,
∴六年级同学赢了k(4k-1)场比赛,
∴六年级同学赢了他们所参加的每一场比赛,从而六年级同学不能赢本年级同学,
∴一共只有1名六年级同学参加比赛,且他就是冠军.
点评 本题考查的是推理与论证,根据题意得出参赛的总场数是解答此题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
3.某厂工人小王某月工作的部分信息如下:
信息一:工作时间:每天上午8:00~12:00,下午13:00~17:00,每月25天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于60件.
生产产品的件数与所用时间之间的关系如下表:
信息三:按件计酬,每生产一件甲产品可得1.5元,每生产一件乙产品可得2.80元.
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分钟?
(2)若小王每月生产甲产品a件,乙产品b件,当a、b分别是多少时,小王收入最多?
信息一:工作时间:每天上午8:00~12:00,下午13:00~17:00,每月25天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于60件.
生产产品的件数与所用时间之间的关系如下表:
| 生产甲产品件数(件) | 生产乙产品件数(件) | 所用总时间(min) |
| 10 | 10 | 350 |
| 30 | 20 | 850 |
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分钟?
(2)若小王每月生产甲产品a件,乙产品b件,当a、b分别是多少时,小王收入最多?
2.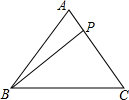 如图,在△ABC中,有一点P在直线AC上移动,若AB=AC=5,BC=6,则BP的最小值为( )
如图,在△ABC中,有一点P在直线AC上移动,若AB=AC=5,BC=6,则BP的最小值为( )
 如图,在△ABC中,有一点P在直线AC上移动,若AB=AC=5,BC=6,则BP的最小值为( )
如图,在△ABC中,有一点P在直线AC上移动,若AB=AC=5,BC=6,则BP的最小值为( )| A. | 4.8 | B. | 5 | C. | 4 | D. | $\sqrt{24}$ |
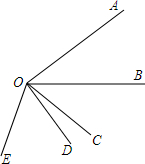 如图,∠A0B=40°,∠B0E是任意一个小于平角的角,射线0C、0D分别平分∠A0E、∠B0E,求∠C0D的度数.
如图,∠A0B=40°,∠B0E是任意一个小于平角的角,射线0C、0D分别平分∠A0E、∠B0E,求∠C0D的度数.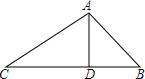 先阅读材料.再解答下面的问题:问题:在△ABC中,AD是边BC上的高,AD=2,DB=2,CD=2$\sqrt{3}$,求∠BAC的度数.
先阅读材料.再解答下面的问题:问题:在△ABC中,AD是边BC上的高,AD=2,DB=2,CD=2$\sqrt{3}$,求∠BAC的度数.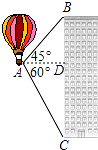 如图,热气球的探测器在点A,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为30米,求这栋楼的高度($\sqrt{3}$取1.73,结果精确到0.1米).
如图,热气球的探测器在点A,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为30米,求这栋楼的高度($\sqrt{3}$取1.73,结果精确到0.1米).