题目内容
9. 小丽想测量学校旗杆的高度,她在地面A点安置侧倾器,测得旗杆顶端C的仰角为α,侧倾器到旗杆底部的距离AD为10米,侧倾器的高度AB为1.5米,那么旗杆的高度CD为( )
小丽想测量学校旗杆的高度,她在地面A点安置侧倾器,测得旗杆顶端C的仰角为α,侧倾器到旗杆底部的距离AD为10米,侧倾器的高度AB为1.5米,那么旗杆的高度CD为( )| A. | (10tanα+1.5)米 | B. | (10cosα+1.5)米 | C. | ($\frac{10}{tanα}$+1.5)米 | D. | ($\frac{10}{sinα}$+1.5)米 |
分析 在直角三角形CBE中,利用锐角三角函数定义表示出CE,由CE+ED求出CD的长即可.
解答  解:在Rt△CBE中,BE=AD=10米,∠CBE=α,
解:在Rt△CBE中,BE=AD=10米,∠CBE=α,
∴CE=10tanα,
则CD=CE+ED=(10tanα+1.5)米.
故选A.
点评 此题考查了解直角三角形的应用-仰角俯角问题,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
14.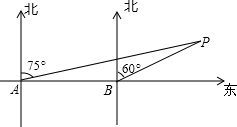 某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,继续航行7海里后,在B处测得小岛P的方位是北偏东60°,则此时轮船与小岛P的距离BP=( )
某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,继续航行7海里后,在B处测得小岛P的方位是北偏东60°,则此时轮船与小岛P的距离BP=( )
 某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,继续航行7海里后,在B处测得小岛P的方位是北偏东60°,则此时轮船与小岛P的距离BP=( )
某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,继续航行7海里后,在B处测得小岛P的方位是北偏东60°,则此时轮船与小岛P的距离BP=( )| A. | 7海里 | B. | 14海里 | C. | 3.5海里 | D. | 4海里 |
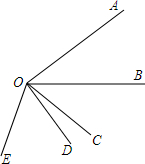 如图,∠A0B=40°,∠B0E是任意一个小于平角的角,射线0C、0D分别平分∠A0E、∠B0E,求∠C0D的度数.
如图,∠A0B=40°,∠B0E是任意一个小于平角的角,射线0C、0D分别平分∠A0E、∠B0E,求∠C0D的度数.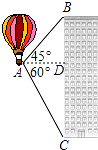 如图,热气球的探测器在点A,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为30米,求这栋楼的高度($\sqrt{3}$取1.73,结果精确到0.1米).
如图,热气球的探测器在点A,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为30米,求这栋楼的高度($\sqrt{3}$取1.73,结果精确到0.1米).