题目内容
15.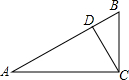 如图,△ABC中,∠ACB=90°,BC=8,AC=12,∠BCD=30°,求线段CD长.
如图,△ABC中,∠ACB=90°,BC=8,AC=12,∠BCD=30°,求线段CD长.
分析 过D作DE⊥AC于E,于是得到DE∥BC,根据平行线的性质得到∠CDE=∠BCD=30°,设CD=x,根据直角三角形的性质得到CE=$\frac{1}{2}$CD=$\frac{1}{2}$x,DE=$\frac{\sqrt{3}}{2}$x,求得AE=12-$\frac{1}{2}$x推出△ABC∽△ADE,根据相似三角形的性质得到$\frac{AC}{AE}=\frac{BC}{DE}$,列方程$\frac{12}{12-\frac{1}{2}x}=\frac{8}{\frac{\sqrt{3}}{2}x}$,即可得到结论.
解答 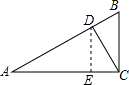 解:过D作DE⊥AC于E,
解:过D作DE⊥AC于E,
∵∠ACB=90°,
∴DE∥BC,
∴∠CDE=∠BCD=30°,
设CD=x,
∴CE=$\frac{1}{2}$CD=$\frac{1}{2}$x,DE=$\frac{\sqrt{3}}{2}$x,
∴AE=12-$\frac{1}{2}$x,
∵DE∥BC,
∴△ABC∽△ADE,
∴$\frac{AC}{AE}=\frac{BC}{DE}$,
∴$\frac{12}{12-\frac{1}{2}x}=\frac{8}{\frac{\sqrt{3}}{2}x}$,
解得:x=$\frac{48(3\sqrt{3}-2)}{25}$.
∴CD=$\frac{48(3\sqrt{3}-2)}{25}$.
点评 本题考查了含30°角的直角三角形的性质,相似三角形的判定和性质,熟记含30°角的直角三角形的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.某厂工人小王某月工作的部分信息如下:
信息一:工作时间:每天上午8:00~12:00,下午13:00~17:00,每月25天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于60件.
生产产品的件数与所用时间之间的关系如下表:
信息三:按件计酬,每生产一件甲产品可得1.5元,每生产一件乙产品可得2.80元.
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分钟?
(2)若小王每月生产甲产品a件,乙产品b件,当a、b分别是多少时,小王收入最多?
信息一:工作时间:每天上午8:00~12:00,下午13:00~17:00,每月25天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于60件.
生产产品的件数与所用时间之间的关系如下表:
| 生产甲产品件数(件) | 生产乙产品件数(件) | 所用总时间(min) |
| 10 | 10 | 350 |
| 30 | 20 | 850 |
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分钟?
(2)若小王每月生产甲产品a件,乙产品b件,当a、b分别是多少时,小王收入最多?
5. 已知二次函数y=x2-2x-3.
已知二次函数y=x2-2x-3.
(1)将y=x2-2x-3化成y=a(x-h)2+k的形式;
(2)与y轴的交点坐标是(0,-3),与x轴的交点坐标是(3,0)(-1,0);
(3)在坐标系中利用描点法画出此抛物线.
(4)不等式x2-2x-3>0的解集是x<-1或x>3.
 已知二次函数y=x2-2x-3.
已知二次函数y=x2-2x-3.(1)将y=x2-2x-3化成y=a(x-h)2+k的形式;
(2)与y轴的交点坐标是(0,-3),与x轴的交点坐标是(3,0)(-1,0);
(3)在坐标系中利用描点法画出此抛物线.
| x | … | … | |||||
| y | … | … |
 如图,△ABC中,∠ACB=90°,AC=BC,AD⊥CD于D,BE⊥CD于E,BE=2.5cm,DE=1.7cm,求AD的长.
如图,△ABC中,∠ACB=90°,AC=BC,AD⊥CD于D,BE⊥CD于E,BE=2.5cm,DE=1.7cm,求AD的长.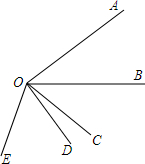 如图,∠A0B=40°,∠B0E是任意一个小于平角的角,射线0C、0D分别平分∠A0E、∠B0E,求∠C0D的度数.
如图,∠A0B=40°,∠B0E是任意一个小于平角的角,射线0C、0D分别平分∠A0E、∠B0E,求∠C0D的度数.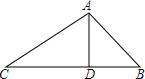 先阅读材料.再解答下面的问题:问题:在△ABC中,AD是边BC上的高,AD=2,DB=2,CD=2$\sqrt{3}$,求∠BAC的度数.
先阅读材料.再解答下面的问题:问题:在△ABC中,AD是边BC上的高,AD=2,DB=2,CD=2$\sqrt{3}$,求∠BAC的度数.