题目内容
4.已知x1、x2是方程x2-2(k+1)x+k2+2=0的另个实数根,且(x1+1)(x2+1)=8.求k的值.分析 根据根与系数的关系可得出x1+x2和x1x2的值,再把(x1+1)(x2+1)=8整理,代入数据进行计算即可.
解答 解:∵x1、x2是方程x2-2(k+1)x+k2+2=0的另个实数根,
∴x1+x2=2(k+1),x1x2=k2+2,
∵(x1+1)(x2+1)=8,
∴x1x2+(x1+x2,)+1=8,
∴2(k+1)+k2+2+1=8,
解得k1=-3,k2=1,
当k=-3时,得方程x2+4x+11=0,△=42-4×11<0,舍去;
当k=1时,得方程x2-4x+3=0,△=(-4)2-4×3>0,
∴k的值为1.
点评 本题考查了根与系数的关系,以及根的判别式,掌握根与系数的关系是解题的关键.

练习册系列答案
相关题目
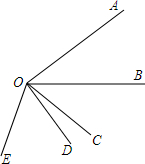 如图,∠A0B=40°,∠B0E是任意一个小于平角的角,射线0C、0D分别平分∠A0E、∠B0E,求∠C0D的度数.
如图,∠A0B=40°,∠B0E是任意一个小于平角的角,射线0C、0D分别平分∠A0E、∠B0E,求∠C0D的度数.