题目内容
10.试写出一个以-1,-3为两根的一元二次方程x2+4x+3=0.分析 根据根与系数的关系:两根之和=-$\frac{b}{a}$,两根之积=$\frac{c}{a}$,首先写出两根之和,再写出两根之积,可直接得到方程.
解答 解:∵-1+(-3)=-4,(-1)×(-3)=3,
∴方程为:x2+4x+3=0,
故答案为:x2+4x+3=0.
点评 此题主要考查了根与系数的关系,将根与方程的系数相结合解题是一种经常使用的解题方法.

练习册系列答案
相关题目
5.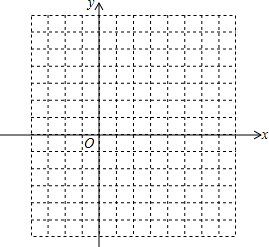 已知二次函数y=x2-2x-3.
已知二次函数y=x2-2x-3.
(1)将y=x2-2x-3化成y=a(x-h)2+k的形式;
(2)与y轴的交点坐标是(0,-3),与x轴的交点坐标是(3,0)(-1,0);
(3)在坐标系中利用描点法画出此抛物线.
(4)不等式x2-2x-3>0的解集是x<-1或x>3.
 已知二次函数y=x2-2x-3.
已知二次函数y=x2-2x-3.(1)将y=x2-2x-3化成y=a(x-h)2+k的形式;
(2)与y轴的交点坐标是(0,-3),与x轴的交点坐标是(3,0)(-1,0);
(3)在坐标系中利用描点法画出此抛物线.
| x | … | … | |||||
| y | … | … |
2.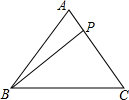 如图,在△ABC中,有一点P在直线AC上移动,若AB=AC=5,BC=6,则BP的最小值为( )
如图,在△ABC中,有一点P在直线AC上移动,若AB=AC=5,BC=6,则BP的最小值为( )
 如图,在△ABC中,有一点P在直线AC上移动,若AB=AC=5,BC=6,则BP的最小值为( )
如图,在△ABC中,有一点P在直线AC上移动,若AB=AC=5,BC=6,则BP的最小值为( )| A. | 4.8 | B. | 5 | C. | 4 | D. | $\sqrt{24}$ |
20.下列结论不正确的是( )
| A. | 若a+2=b+2,则a=b | B. | 若ac=bc,则a=b | ||
| C. | 若ax=b(a≠0),则x=$\frac{b}{a}$ | D. | 若$\frac{a}{c}=\frac{b}{c}$,则a=b |
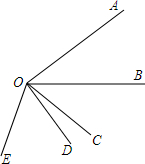 如图,∠A0B=40°,∠B0E是任意一个小于平角的角,射线0C、0D分别平分∠A0E、∠B0E,求∠C0D的度数.
如图,∠A0B=40°,∠B0E是任意一个小于平角的角,射线0C、0D分别平分∠A0E、∠B0E,求∠C0D的度数.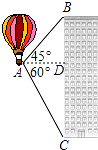 如图,热气球的探测器在点A,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为30米,求这栋楼的高度($\sqrt{3}$取1.73,结果精确到0.1米).
如图,热气球的探测器在点A,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为30米,求这栋楼的高度($\sqrt{3}$取1.73,结果精确到0.1米).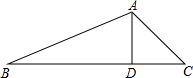 如图,AD⊥BC于D,BD=AC+DC,若∠BAC=120°,那么∠C的度数为40°.
如图,AD⊥BC于D,BD=AC+DC,若∠BAC=120°,那么∠C的度数为40°.