题目内容
2.一个不透明的盒子中装有2个白球,5个红球和8个黄球,这些球除颜色外都相同,现从这个盒子中随机摸出一个球,摸到红球的概率为( )| A. | $\frac{8}{15}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{15}$ | D. | $\frac{1}{15}$ |
分析 根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.
解答 解:根据题意可得:一个不透明的盒子中装有2个白球,5个红球和8个黄球,共15个,
摸到红球的概率为$\frac{5}{15}$=$\frac{1}{3}$,
故选:B.
点评 此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列格式中正确的是( )
| A. | $\sqrt{25}$=±$\sqrt{5}$ | B. | (-$\sqrt{0.36}$)2=-0.36 | C. | $\root{3}{64}$=4 | D. | $\sqrt{(-3)^{2}}$=3 |
11.在平面内,下列命题为真命题的是( )
| A. | 四条边相等的四边形是菱形 | B. | 对角线垂直的四边形是菱形 | ||
| C. | 对角线相等的四边形是矩形 | D. | 四个角相等的四边形是正方形 |
20.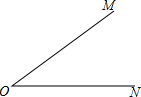 已知∠MON=36°,先以O为圆心,任意长为半径画弧,分别交OM、ON于点A、B,再以A为圆心,AB长为半径画弧,交ON于点C,度量∠ACO的度数为( )
已知∠MON=36°,先以O为圆心,任意长为半径画弧,分别交OM、ON于点A、B,再以A为圆心,AB长为半径画弧,交ON于点C,度量∠ACO的度数为( )
 已知∠MON=36°,先以O为圆心,任意长为半径画弧,分别交OM、ON于点A、B,再以A为圆心,AB长为半径画弧,交ON于点C,度量∠ACO的度数为( )
已知∠MON=36°,先以O为圆心,任意长为半径画弧,分别交OM、ON于点A、B,再以A为圆心,AB长为半径画弧,交ON于点C,度量∠ACO的度数为( )| A. | 36° | B. | 72° | C. | 108° | D. | 180° |
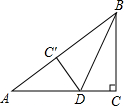 如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是6cm2.
如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是6cm2.