题目内容
20．
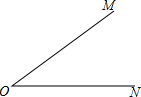已知∠MON=36°，先以O为圆心，任意长为半径画弧，分别交OM、ON于点A、B，再以A为圆心，AB长为半径画弧，交ON于点C，度量∠ACO的度数为（ ）| A． | 36° | B． | 72° | C． | 108° | D． | 180° |
分析 先根据题意画出图形，再根据根据等腰三角形的性质，求得∠ACB=∠ABC=72°，进而得到∠ACO=180°-72°=108°．
解答 
解：如图所示，∵AO=BO，∠AOB=36°，
∴△AOB中，∠ABC=72°，
∵AB=AC，
∴△ABC中，∠ACB=∠ABC=72°，
∴∠ACO=180°-72°=108°．
故选：C．
点评 本题主要考查了基本作图和等腰三角形的性质的运用，解决问题的关键是掌握：等腰三角形的两个底角相等．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
2．一个不透明的盒子中装有2个白球，5个红球和8个黄球，这些球除颜色外都相同，现从这个盒子中随机摸出一个球，摸到红球的概率为（ ）
| A． | $\frac{8}{15}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{15}$ | D． | $\frac{1}{15}$ |
3．对于任意实数m，点P（m-2，9-3m）不可能在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
如图，图形我们把它称为“8字形”，请说明∠A+∠B=∠C+∠D．
15．把2张形状大小完全相同的小长方形卡片（如图①）不重叠地放在一个底面为长方形（长为m，宽为n）的盒子底部（如图②），盒子底面未被卡片覆盖的部分用阴影表示．阴影部分刚好能分割成两张形状大小不同的小长方形卡片（如图③），则分割后的两个阴影长方形的周长和是（ ）
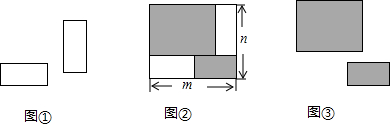
| A． | 4m | B． | 2（m+n） | C． | 4n | D． | 4（m-n） |
5．（1）特例导航：请根据所给的运算程序完成填空．
（2）探索与归纳：
如果把你最初任意选择的三个不同的数字分别用a、b、c表示，且a≠b≠c，请再次根据所给运算程序完成填空．
归纳：
从1～9这9个数字中，任意选择3个不同的数字，由这三个数字组成6个不同的三位数（个位数字、十位数字、百位数字互相不重复），把这6个三位数相加，然后用所得的和除以这三个数字的和，结果是222．
（2）探索与归纳：
| 运算程序 | 例如 | 按左侧的形式完成你的举例 |
| ①从1～9这9个数字中，任意选择3个不同的数字 | 3、2、5 | 1、2、3 |
| ②由这三个数字组成6个不同的三位数（个位数字、十位数字、百位数字互相不重复） | 325、352、253、235、523、532 | 123、132、213、231、312、321 |
| ③将②中这6个三位数相加 | 325+352+253+235+523+532=a= 2220 | 1332 |
| ④用③所得的和除以这三个数字的和，得结果 | a÷（3+2+5）= 222 | 222 |
| 运算程序 | 运算过程 |
| ①从1～9这9个数字中，任意选择3个不同的数字 | a、b、c，且a≠b≠c |
| ②由这三个数字组成6个不同的三位数（个位数字、十位数字、百位数字互相不重复） | |
| ③将②中这6个三位数相加 | |
| ④用③所得的和除以这三个数字的和，得结果 |
从1～9这9个数字中，任意选择3个不同的数字，由这三个数字组成6个不同的三位数（个位数字、十位数字、百位数字互相不重复），把这6个三位数相加，然后用所得的和除以这三个数字的和，结果是222．
