题目内容
10.若规定:sin(α+β)=sinα•sinβ+cosα•sinβ,试确定sin75°+sin90°的值.分析 根据给出的公式,将75°和90°化为特殊角即可求出答案.
解答 解:原式=sin(30°+45°)+sin(30°+60°)
=sin30°•cos45°+cos30°•sin45°+sin30°•cos60°+cos30°•sin60°
=$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{2}}{2}$+$\frac{1}{2}$×$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{3}}{2}$
=$\frac{\sqrt{2}}{4}$+$\frac{\sqrt{6}}{4}$+$\frac{1}{4}$+$\frac{3}{4}$
=$\frac{4+\sqrt{2}+\sqrt{6}}{4}$
点评 本题考查特殊角的三角函数值,解题的关键是将75°和90°化为特殊角进行计算,本题属于基础题型.

练习册系列答案
相关题目
20. 数轴上的A,B,C,D四个点中,离表示-$\sqrt{2}$的点最接近的是( )
数轴上的A,B,C,D四个点中,离表示-$\sqrt{2}$的点最接近的是( )
 数轴上的A,B,C,D四个点中,离表示-$\sqrt{2}$的点最接近的是( )
数轴上的A,B,C,D四个点中,离表示-$\sqrt{2}$的点最接近的是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
1.已知二次函数y=x2-bx-1(b>1),则下列说法正确的是( )
| A. | 无法判断其图象与x轴是否有交点 | |
| B. | 其对称轴与x轴交于负半轴 | |
| C. | 若点(m,n)在y=x2-bx-1的图象上,则n≥-1 | |
| D. | 若点(-3,y1)、(2,y2)都在y=x2-bx-1的图象上,则y1>y2 |
15. 如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,则下列说法正确的是( )
如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,则下列说法正确的是( )
 如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,则下列说法正确的是( )
如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,则下列说法正确的是( )| A. | AD垂直FE | B. | AD平分EF | C. | EF垂直平分AD | D. | AD垂直平分EF |
2.一个不透明的盒子中装有2个白球,5个红球和8个黄球,这些球除颜色外都相同,现从这个盒子中随机摸出一个球,摸到红球的概率为( )
| A. | $\frac{8}{15}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{15}$ | D. | $\frac{1}{15}$ |
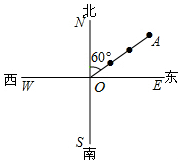 如图,货轮O在航行过程中,在它的北偏东60°方向上,与之相距30海里处发现灯塔A,同时在它的南偏东30°方向上,与之相距20海里处发现货轮B,在它的西南方向上发现客轮C,按下列要求画出.
如图,货轮O在航行过程中,在它的北偏东60°方向上,与之相距30海里处发现灯塔A,同时在它的南偏东30°方向上,与之相距20海里处发现货轮B,在它的西南方向上发现客轮C,按下列要求画出.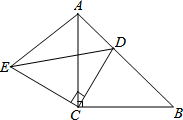 如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证:
如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证: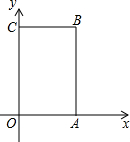 如图,长方形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(2,0)、(0,4).
如图,长方形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(2,0)、(0,4). 如图,图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D.
如图,图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D.