题目内容
2．
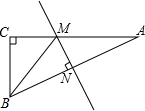如图，在Rt△ABC中，∠C=90°，AC=12，AB=13，AB边的垂直平分线分别交AB、AC于N、M两点，则△BCM的周长为（ ）| A． | 18 | B． | 16 | C． | 17 | D． | 无法确定 |
分析 根据勾股定理求出BC的长，根据线段垂直平分线的性质得到MB=MA，根据三角形的周长的计算方法代入计算即可．
解答 解：在Rt△ABC中，∠C=90°，AC=12，AB=13，
由勾股定理得，BC=5，
∵MN是AB的垂直平分线，
∴MB=MA，
△BCM的周长=BC+CM+MB=BC+CM+MA=BC+CA=17，
故选：C．
点评 本题考查的是线段的垂直平分线的性质等几何知识，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
练习册系列答案
科学实验活动册系列答案
相关题目
某冷饮点一天售出各种口味雪糕数量的扇形统计图如图所示，其中售出红豆口味的雪糕200支．
13．
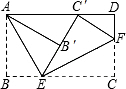将矩形ABCD按如图所示的方式折叠，AE、EF为折痕，∠BAE=30°，AB=$\sqrt{3}$，折叠后，点C落在AD边上的C′处，并且点B落在EC′边上的B′处，则BC的长为（ ）
将矩形ABCD按如图所示的方式折叠，AE、EF为折痕，∠BAE=30°，AB=$\sqrt{3}$，折叠后，点C落在AD边上的C′处，并且点B落在EC′边上的B′处，则BC的长为（ ）| A． | $\sqrt{3}$ | B． | 2$\sqrt{3}$ | C． | 2 | D． | 3 |
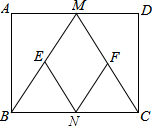如图，在矩形ABCD中，M、N分别是边AD、BC的中点，E、F分别是边BM、CM的中点，当AB：AD=1：2时，四边形MENF是正方形．
7．下列能用平方差公式计算的是（ ）
| A． | （-x+y）（x-y） | B． | （y-1）（-1-y） | C． | （x-2）（x+1） | D． | （2x+y）（2y-x） |
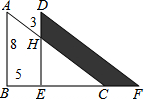如图，原来是重叠的两个直角三角形，将其中一个三角形沿着BC方向平移线段BE的距离，就得到此图形，下列结论正确的有（ ）