题目内容
13.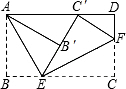 将矩形ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=$\sqrt{3}$,折叠后,点C落在AD边上的C′处,并且点B落在EC′边上的B′处,则BC的长为( )
将矩形ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=$\sqrt{3}$,折叠后,点C落在AD边上的C′处,并且点B落在EC′边上的B′处,则BC的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 3 |
分析 由折叠的性质得出△ABE≌△AB′E,△EC′F≌△ECF,得出BE=B′E,∠B=∠AB′E=90°,AC′=AE,得出BE=1,证出△AEC′是等边三角形,得出EC=EC′=2,即可求出BC.
解答 解:∵△ABE和△AB′E对折,
∴△ABE≌△AB′E,
∴BE=B′E,∠B=∠AB′E=90°,
∵∠BAE=30°,AB=$\sqrt{3}$,
∴BE=1,
∵△AB′C′≌△AB′E,
∴AC′=AE,
又∵∠AEC′=∠AEB=60°,
∴△AEC′是等边三角形,EC′=AE=2,
∵EC=EC′=2,
∴BC=2+1=3,
故选:D.
点评 本题考查了翻折变换的性质、全等三角形的性质、等边三角形的判定与性质;熟练掌握翻折变换的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
1.要使分式$\frac{2}{x-2}$有意义,x必须满足的条件是( )
| A. | x≠0 | B. | x≠2 | C. | x=2 | D. | x>2 |
8.有若干张面积分别为a2、b2、ab的正方形和长方形纸片,小明从中抽取了1张面积为b2的正方形纸片,6张面积为ab的长方形纸片.若他想拼成一个大正方形,则还需要抽取面积为a2的正方形纸片( )
| A. | 4张 | B. | 8张 | C. | 9张 | D. | 10张 |
2.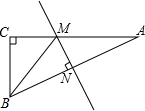 如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )
如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )
 如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )
如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )| A. | 18 | B. | 16 | C. | 17 | D. | 无法确定 |

 如图所示,图1是一个长为2m,宽为2n的长方形,沿图中的虚线剪成四个完全相同的小长方形,再按图2围成一个较大的正方形.
如图所示,图1是一个长为2m,宽为2n的长方形,沿图中的虚线剪成四个完全相同的小长方形,再按图2围成一个较大的正方形.