题目内容
9.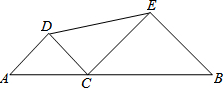 如图,线段AB的长为10,C为AB上的一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角△ACD和△BCE,那么DE长的最小值是5.
如图,线段AB的长为10,C为AB上的一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角△ACD和△BCE,那么DE长的最小值是5.
分析 设AC=x,BC=10-x,根据等腰直角三角形性质,得出CD=$\frac{\sqrt{2}}{2}$,CD′=$\frac{\sqrt{2}}{2}$(10-x),根据勾股定理然后用配方法即可求解.
解答 解:设AC=x,BC=10-x,
∵△ABC,△BCD′均为等腰直角三角形,
∴CD=$\frac{\sqrt{2}}{2}$x,CD′=$\frac{\sqrt{2}}{2}$(10-x),
∵∠ACD=45°,∠BCD′=45°,
∴∠DCE=90°,
∴DE2=CD2+CE2=$\frac{1}{2}$x2+$\frac{1}{2}$(10-x)2=x2-10x+50=(x-5)2+25,
∴当x取5时,DE取最小值,最小值为:5,
故答案为:5.
点评 本题主要考查了二次函数最值及等腰直角三角形,掌握用配方法求二次函数最值是解答此题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
20.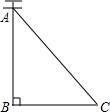 如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
 如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )| A. | $\frac{6}{sin50°}$米 | B. | $\frac{6}{tan50°}$米 | C. | 6cos50°米 | D. | $\frac{6}{cos50°}$米 |
17.下面几组数:①7,8,9;②12,9,15;③a2,a2+1,a2+2;④m2+n2,m2-n2,2mn(m、n均为正整数,m>n),其中能组成直角三角形的三边长的是( )
| A. | ①② | B. | ②③ | C. | ①③ | D. | ②④ |
1.若平行四边形中两个内角的度数比为1:2,则其中较小的内角是( )
| A. | 60° | B. | 90° | C. | 120° | D. | 45° |
 在RtABC中,∠C=90°,AC=BC=$\sqrt{2}$(如图),若将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,联结C′B,则C′B的长为$\sqrt{3}$-1.
在RtABC中,∠C=90°,AC=BC=$\sqrt{2}$(如图),若将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,联结C′B,则C′B的长为$\sqrt{3}$-1.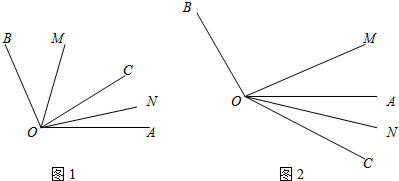
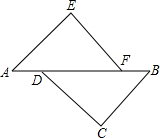 如图,AE∥BC,AE=BC,点D、F在AB上,且AD=BF.
如图,AE∥BC,AE=BC,点D、F在AB上,且AD=BF.