题目内容
6.已知:在Rt△ABC中,∠C=90°,∠A=60°,a=$\sqrt{6}$,求b、c的长.分析 根据三角函数求出b的长,再利用勾股定理求出c的长.
解答  解:如图:∵$\frac{a}{b}$=tan60°,
解:如图:∵$\frac{a}{b}$=tan60°,
∴b=$\frac{a}{tan60°}$=$\frac{\sqrt{6}}{\sqrt{3}}$=$\sqrt{2}$;
∴c=$\sqrt{6+2}$=$\sqrt{8}$=2$\sqrt{2}$.
点评 本题考查了勾股定理、含30°角的直角三角形,熟练利用三角函数是解题的关键.

练习册系列答案
相关题目
17.下面几组数:①7,8,9;②12,9,15;③a2,a2+1,a2+2;④m2+n2,m2-n2,2mn(m、n均为正整数,m>n),其中能组成直角三角形的三边长的是( )
| A. | ①② | B. | ②③ | C. | ①③ | D. | ②④ |
1.若平行四边形中两个内角的度数比为1:2,则其中较小的内角是( )
| A. | 60° | B. | 90° | C. | 120° | D. | 45° |
11.如图1,在五边形ABCDE中,AE∥BC,∠A=∠C.
(1)猜想AB与CD之间的位置关系,并说明理由;
(2)延长DE至F,连接BE,如图2,若∠1=∠3,∠AEF=2∠2,求证:∠AED=∠C.
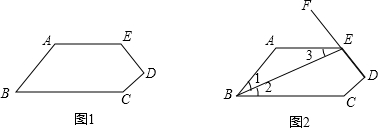
(1)猜想AB与CD之间的位置关系,并说明理由;
(2)延长DE至F,连接BE,如图2,若∠1=∠3,∠AEF=2∠2,求证:∠AED=∠C.

15.如果分式$\frac{2x}{x-y}$中的x、y都缩小到原来的$\frac{1}{3}$倍,那么分式的值( )
| A. | 扩大到原来的3倍 | B. | 扩大到原来的6倍 | ||
| C. | 不变 | D. | 缩小到原来的$\frac{1}{3}$倍 |
 如图所示,三角形OAB的顶点B的坐标为(4,0),把三角形OAB沿x轴向右平移得到三角形CDE,如果CB=1,那么OE的长为7.
如图所示,三角形OAB的顶点B的坐标为(4,0),把三角形OAB沿x轴向右平移得到三角形CDE,如果CB=1,那么OE的长为7.
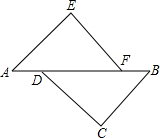 如图,AE∥BC,AE=BC,点D、F在AB上,且AD=BF.
如图,AE∥BC,AE=BC,点D、F在AB上,且AD=BF.