题目内容
3.是否存在整数m,使关于x的方程5x-2m=3x-6m+2的解满足-3≤x<2?若存在,求出m的值;若不存在,请说明理由.分析 首先解方程利用m表示出x,然后根据x的范围得到一个关于m的不等式组,求得m的范围,然后确定整数解即可.
解答 解:存在.
解方程5x-2m=3x-6m+2,得x=-2m+1,
根据题意得:-3≤-2m+1<2.
解得:-$\frac{1}{2}$<m≤2.
则整数解是0,1 2.
点评 本题考查了一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13. 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交FG于点P,则DP等于( )
如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交FG于点P,则DP等于( )
 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交FG于点P,则DP等于( )
如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交FG于点P,则DP等于( )| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 2 | D. | 1 |
15.解方程$1-\frac{x+3}{3}=\frac{x}{2}$时,去分母后可以得到( )
| A. | 1-x-3=3x | B. | 6-2x-6=3x | C. | 6-x+3=3x | D. | 1-x+3=3x |
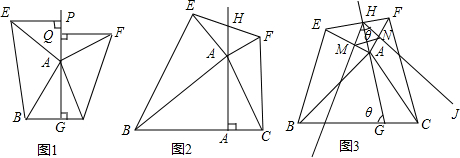
 已知直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,BC=DC=5,点P在BC上移动,则当PA+PD取最小值时,BP长为( )
已知直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,BC=DC=5,点P在BC上移动,则当PA+PD取最小值时,BP长为( )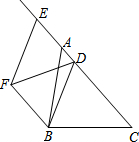 如图,△ABC中,AB=10,sin∠BAC=$\frac{3}{5}$,点D为边AC上一点,点E为CA延长线上一点,且$\frac{AD}{AE}$=$\frac{1}{2}$,以DB、DE为边作?BDEF,则当对角线DF的长取得最小值时,BD的长为8.
如图,△ABC中,AB=10,sin∠BAC=$\frac{3}{5}$,点D为边AC上一点,点E为CA延长线上一点,且$\frac{AD}{AE}$=$\frac{1}{2}$,以DB、DE为边作?BDEF,则当对角线DF的长取得最小值时,BD的长为8.