题目内容
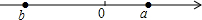 有理数a,b在数轴上表示如图所示,则下列各式正确的个数为( )
有理数a,b在数轴上表示如图所示,则下列各式正确的个数为( )①b3>0;②ab<0;③a+b<0;④b-a>0.
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:数轴
专题:
分析:根据图示知b<0<a,并且|a|<|b|.然后由不等式的性质进行解答.
解答:解:由题意得,b<0<a,且|a|<|b|.
A∵b<0,
∴b3<0,故本选项错误;
B、∵b<0<a,
∴ab<0,故本选项正确;
C、∵a>0,b<0,且|a|<|b|,
∴a+b<0,故本选项正确;
D、∵a>0,
∴-a<0,
∵b<0,
∴b-a=b+(-a)<0,故本选项错误;
故选B.
A∵b<0,
∴b3<0,故本选项错误;
B、∵b<0<a,
∴ab<0,故本选项正确;
C、∵a>0,b<0,且|a|<|b|,
∴a+b<0,故本选项正确;
D、∵a>0,
∴-a<0,
∵b<0,
∴b-a=b+(-a)<0,故本选项错误;
故选B.
点评:此题考查数轴的知识,属于基础题,解答本题的关键是通过图形得出a为正数,b为负数,且|a|<|b|,难度一般.

练习册系列答案
相关题目
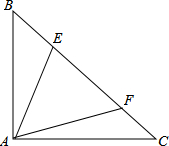 如图,在Rt△ABC中,∠BAC=90°,AB=AC,E、F分别是BC上两点,满足∠EAF=45°,若AB=
如图,在Rt△ABC中,∠BAC=90°,AB=AC,E、F分别是BC上两点,满足∠EAF=45°,若AB=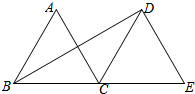 如图,△ABC和△DCE都是边长为4的等边三角形,点B、C、E在同一条直线上,连接BD,则BD的长为
如图,△ABC和△DCE都是边长为4的等边三角形,点B、C、E在同一条直线上,连接BD,则BD的长为 某居民区一处圆形下水管道破裂,维修人员准备更换一段新管道,如图,污水水面宽度为60cm,水面到管道顶部距离为10cm,则修理人员应准备
某居民区一处圆形下水管道破裂,维修人员准备更换一段新管道,如图,污水水面宽度为60cm,水面到管道顶部距离为10cm,则修理人员应准备 如图,在△ABC中,∠C=90°,∠B=28°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E,求
如图,在△ABC中,∠C=90°,∠B=28°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E,求