题目内容
 某居民区一处圆形下水管道破裂,维修人员准备更换一段新管道,如图,污水水面宽度为60cm,水面到管道顶部距离为10cm,则修理人员应准备
某居民区一处圆形下水管道破裂,维修人员准备更换一段新管道,如图,污水水面宽度为60cm,水面到管道顶部距离为10cm,则修理人员应准备考点:垂径定理的应用,勾股定理
专题:
分析:连接OA作弦心距,就可以构造成直角三角形.设出半径弦心距也可以得到,利用勾股定理就可以求出了.
解答:解:如图,过O作OC⊥AB于C,连接AO,

∴AC=
AB=
×60=30,
CO=AO-10,
在Rt△AOC中,AO2=AC2+OC2,
AO2=302+(AO-10)2,
解得AO=50cm.
∴内径为2×50=100cm.
故答案为:100.

∴AC=
| 1 |
| 2 |
| 1 |
| 2 |
CO=AO-10,
在Rt△AOC中,AO2=AC2+OC2,
AO2=302+(AO-10)2,
解得AO=50cm.
∴内径为2×50=100cm.
故答案为:100.
点评:考查了垂径定理的应用和勾股定理,本题的难点在于构造出直角三角形,内径指的是直径,这一点学生可能会出错.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
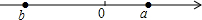 有理数a,b在数轴上表示如图所示,则下列各式正确的个数为( )
有理数a,b在数轴上表示如图所示,则下列各式正确的个数为( )①b3>0;②ab<0;③a+b<0;④b-a>0.
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,已知矩形ABCD的边AB=3厘米,AD=4厘米.现以点A为圆心,4厘米为半径作圆A,点B、C、D中在圆A外的有( )
如图,已知矩形ABCD的边AB=3厘米,AD=4厘米.现以点A为圆心,4厘米为半径作圆A,点B、C、D中在圆A外的有( )| A、0点 | B、1点 | C、2点 | D、3点 |
 如图,在△ABC中,∠ACB=90°,AC=BC,点P在AB上,AD⊥CP于D,BE⊥CP于E,已知CD=3cm,求BE的长.
如图,在△ABC中,∠ACB=90°,AC=BC,点P在AB上,AD⊥CP于D,BE⊥CP于E,已知CD=3cm,求BE的长.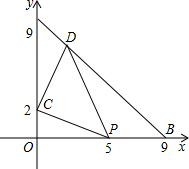 如图,在△AOB中,OA=0B=9,点C的坐标为(0,2),点P是OB上一动点,连接CP,将CP绕C点逆时针旋转90°得到线段CD,使点D恰好落在AB上,求点D的坐标.
如图,在△AOB中,OA=0B=9,点C的坐标为(0,2),点P是OB上一动点,连接CP,将CP绕C点逆时针旋转90°得到线段CD,使点D恰好落在AB上,求点D的坐标.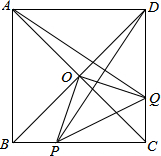 如图,O是正方形ABCD对角线的交点,Q是DC上任意一点,过点D作DE⊥AQ交BC于点P,求证:△OPQ是等腰直角三角形.
如图,O是正方形ABCD对角线的交点,Q是DC上任意一点,过点D作DE⊥AQ交BC于点P,求证:△OPQ是等腰直角三角形.