题目内容
已知直线y=(a+2)x-4a+4.
(1)a为何值时,这条直线经过原点?
(2)a为何值时,这条直线与y轴有交点(0,-2)?
(3)a为何值时,直线过点(1,0)?
(4)a为何值时,直线平行于直线y=-x?
(1)a为何值时,这条直线经过原点?
(2)a为何值时,这条直线与y轴有交点(0,-2)?
(3)a为何值时,直线过点(1,0)?
(4)a为何值时,直线平行于直线y=-x?
考点:一次函数图象上点的坐标特征
专题:
分析:(1)把点(0,0)代入该函数关系式,列出关于a的一元一次方程,通过解该方程来求a的值;
(2)把点(0,-2)代入该函数关系式,列出关于a的一元一次方程,通过解该方程来求a的值;
(3)把点(1,0)代入该函数关系式,列出关于a的一元一次方程,通过解该方程来求a的值;
(4)两直线平行,自变量x的系数相等.
(2)把点(0,-2)代入该函数关系式,列出关于a的一元一次方程,通过解该方程来求a的值;
(3)把点(1,0)代入该函数关系式,列出关于a的一元一次方程,通过解该方程来求a的值;
(4)两直线平行,自变量x的系数相等.
解答:解:(1)把点(0,0)代入y=(a+2)x-4a+4,得
0=-4a+4,
解得 a=1.
即当a=1时,这条直线经过原点;
(2)把点(0,-2)代入y=(a+2)x-4a+4,得
-2=-4a+4,
解得 a=
.
即当a=
时,这条直线与y轴有交点(0,-2);
(3)把点(1,0)代入y=(a+2)x-4a+4,得
0=-(a+2)-4a+4,
解得 a=
.
即当a=
时,这条直线与y轴有交点(1,0);
(4)依题意得 a+2=-1,
解得 a=-3.
即a=-3时,直线平行于直线y=-x.
0=-4a+4,
解得 a=1.
即当a=1时,这条直线经过原点;
(2)把点(0,-2)代入y=(a+2)x-4a+4,得
-2=-4a+4,
解得 a=
| 3 |
| 2 |
即当a=
| 3 |
| 2 |
(3)把点(1,0)代入y=(a+2)x-4a+4,得
0=-(a+2)-4a+4,
解得 a=
| 2 |
| 5 |
即当a=
| 2 |
| 5 |
(4)依题意得 a+2=-1,
解得 a=-3.
即a=-3时,直线平行于直线y=-x.
点评:本题考查了一次函数图象上点的坐标特征.经过函数的某点一定在函数的图象上.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
若函数y=kx+b的图象经过A(1,m),B(m,-1)(其中m>1),则k,b的符号为( )
| A、k>0,b>0 |
| B、k>0,b<0 |
| C、k<0,b>0 |
| D、k<0,b<0 |
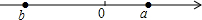 有理数a,b在数轴上表示如图所示,则下列各式正确的个数为( )
有理数a,b在数轴上表示如图所示,则下列各式正确的个数为( )①b3>0;②ab<0;③a+b<0;④b-a>0.
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,?ABCD中,BD是对角线,AE⊥BD于E,CF⊥BD于F.若∠ABE=47°,求∠DCF.
如图,?ABCD中,BD是对角线,AE⊥BD于E,CF⊥BD于F.若∠ABE=47°,求∠DCF.