题目内容
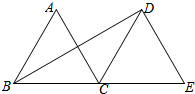如图，△ABC和△DCE都是边长为4的等边三角形，点B、C、E在同一条直线上，连接BD，则BD的长为考点：勾股定理,等边三角形的性质
专题：
分析：过点D作DF⊥EC于点F，利用正三角形的性质得出CF，BF的长，再利用勾股定理求出DF，BD的长即可．
解答：
解：过点D作DF⊥EC于点F，
∵△ABC和△DCE都是边长为4的等边三角形，DF⊥BC，
∴FC=2，CD=4，则BF=6，
在Rt△DFC中，
DF=
=
=2
，
在Rt△BDF中，
BD=
=
=4
．
故答案为：4
．
解：过点D作DF⊥EC于点F，∵△ABC和△DCE都是边长为4的等边三角形，DF⊥BC，
∴FC=2，CD=4，则BF=6，
在Rt△DFC中，
DF=
| DC2-FC2 |
| 42-22 |
| 3 |
在Rt△BDF中，
BD=
| BF2+DF2 |
62+(2
|
| 3 |
故答案为：4
| 3 |
点评：此题主要考查了勾股定理以及等边三角形的性质，得出DF的长是解题关键．
练习册系列答案
相关题目
如图，?ABCD中，BD是对角线，AE⊥BD于E，CF⊥BD于F．若∠ABE=47°，求∠DCF．
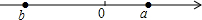有理数a，b在数轴上表示如图所示，则下列各式正确的个数为（ ）①b3＞0；②ab＜0；③a+b＜0；④b-a＞0．
| A、1个 | B、2个 | C、3个 | D、4个 |
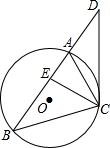如图，已知CD是△ABC的外接圆的切线，C为切点，BA的延长线与切线CD相交于点D，点E在边AB上，且DE=DC．求证：CE平分∠ACB．
如图，在△ABC中，∠ACB=90°，AC=BC，点P在AB上，AD⊥CP于D，BE⊥CP于E，已知CD=3cm，求BE的长．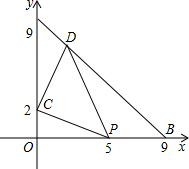
如图，在△AOB中，OA=0B=9，点C的坐标为（0，2），点P是OB上一动点，连接CP，将CP绕C点逆时针旋转90°得到线段CD，使点D恰好落在AB上，求点D的坐标．