题目内容
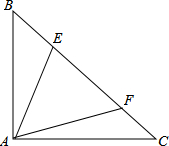 如图,在Rt△ABC中,∠BAC=90°,AB=AC,E、F分别是BC上两点,满足∠EAF=45°,若AB=
如图,在Rt△ABC中,∠BAC=90°,AB=AC,E、F分别是BC上两点,满足∠EAF=45°,若AB=| 72 |
考点:旋转的性质,全等三角形的判定与性质
专题:
分析:将△ABE绕点A顺时针旋转90°得△ACG,根据旋转的性质得AG=AE,CG=BE,∠1=∠B,∠EAG=90°,∠FCG=∠ACB+∠1=∠ACB+∠B=90°,根据勾股定理有FG2=FC2+CG2=BE2+FC2;再根据∠EAF=45°,易证得△AGF≌△AEF,则有FG=EF,即可得到BE、CF、EF之间的数量关系,进而在求出BC的长,即可得出利用勾股定理求出EF,CF的长.
解答:解:∵∠BAC=90°,AB=AC,
∴将△ABE绕点A顺时针旋转90°得△ACG,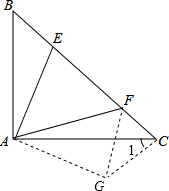
连FG,如图,
∴AG=AE,CG=BE,∠1=∠B,∠EAG=90°,
∴∠FCG=∠ACB+∠1=∠ACB+∠B=90°,
∴FG2=FC2+CG2=BE2+FC2;
又∵∠EAF=45°,而∠EAG=90°,
∴∠GAF=90°-45°=45°,
在△AGF和△AEF中
∴△AGF≌△AEF(SAS),
∴FG=EF,
∴EF2=BE2+FC2,
∵AB=
,BE=3,AB=AC,
∴BC=
=12,
∴EC=9,设FC=x,则EF=9-x,
∴(9-x)2=32+x2,
解得:x=4,则EF=5,
即EF的长为5,CF的长为4.
∴将△ABE绕点A顺时针旋转90°得△ACG,

连FG,如图,
∴AG=AE,CG=BE,∠1=∠B,∠EAG=90°,
∴∠FCG=∠ACB+∠1=∠ACB+∠B=90°,
∴FG2=FC2+CG2=BE2+FC2;
又∵∠EAF=45°,而∠EAG=90°,
∴∠GAF=90°-45°=45°,
在△AGF和△AEF中
|
∴△AGF≌△AEF(SAS),
∴FG=EF,
∴EF2=BE2+FC2,
∵AB=
| 72 |
∴BC=
| 72+72 |
∴EC=9,设FC=x,则EF=9-x,
∴(9-x)2=32+x2,
解得:x=4,则EF=5,
即EF的长为5,CF的长为4.
点评:本题考查了勾股定理以及三角形全等的判定与性质、旋转的性质,得出△AGF≌△AEF是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数y=kx+b的图象经过A(1,m),B(m,-1)(其中m>1),则k,b的符号为( )
| A、k>0,b>0 |
| B、k>0,b<0 |
| C、k<0,b>0 |
| D、k<0,b<0 |
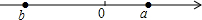 有理数a,b在数轴上表示如图所示,则下列各式正确的个数为( )
有理数a,b在数轴上表示如图所示,则下列各式正确的个数为( )①b3>0;②ab<0;③a+b<0;④b-a>0.
| A、1个 | B、2个 | C、3个 | D、4个 |
已知抛物线y=-x2+bx+c的顶点坐标为(1,2),那么该抛物线有( )
| A、最大值2 | B、最小值2 |
| C、最大值1 | D、最小值1 |
 如图,在△ABC中,∠ACB=90°,AC=BC,点P在AB上,AD⊥CP于D,BE⊥CP于E,已知CD=3cm,求BE的长.
如图,在△ABC中,∠ACB=90°,AC=BC,点P在AB上,AD⊥CP于D,BE⊥CP于E,已知CD=3cm,求BE的长.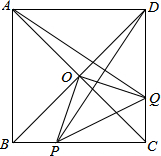 如图,O是正方形ABCD对角线的交点,Q是DC上任意一点,过点D作DE⊥AQ交BC于点P,求证:△OPQ是等腰直角三角形.
如图,O是正方形ABCD对角线的交点,Q是DC上任意一点,过点D作DE⊥AQ交BC于点P,求证:△OPQ是等腰直角三角形.