题目内容
 如图,在△ABC中,∠C=90°,∠B=28°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E,求
如图,在△ABC中,∠C=90°,∠B=28°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E,求 |
| AD |
 |
| DE |
考点:圆心角、弧、弦的关系
专题:计算题
分析:连接CD,如图,利用互余计算出∠A=62°,则∠A=∠ADC=62°,再根据三角形内角和定理计算出∠ACD=56°,接着利用互余计算出∠DCE=34°,然后根据圆心角的度数等于它所对弧的度数求解.
解答:解: 连接CD,如图,
连接CD,如图,
∵∠C=90°,∠B=28°,
∴∠A=90°-28°=62°,
∵CA=CD,
∴∠A=∠ADC=62°,
∴∠ACD=180°-2×62°=56°
∴
的度数为56°;
∵∠DCE=90°-∠ACD=34°,
∴
的度数为34°.
 连接CD,如图,
连接CD,如图,∵∠C=90°,∠B=28°,
∴∠A=90°-28°=62°,
∵CA=CD,
∴∠A=∠ADC=62°,
∴∠ACD=180°-2×62°=56°
∴
 |
| AD |
∵∠DCE=90°-∠ACD=34°,
∴
 |
| DE |
点评:本题考查了圆心角、弧、弦的关系:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.

练习册系列答案
相关题目
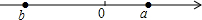 有理数a,b在数轴上表示如图所示,则下列各式正确的个数为( )
有理数a,b在数轴上表示如图所示,则下列各式正确的个数为( )①b3>0;②ab<0;③a+b<0;④b-a>0.
| A、1个 | B、2个 | C、3个 | D、4个 |
已知抛物线y=-x2+bx+c的顶点坐标为(1,2),那么该抛物线有( )
| A、最大值2 | B、最小值2 |
| C、最大值1 | D、最小值1 |
 如图,已知矩形ABCD的边AB=3厘米,AD=4厘米.现以点A为圆心,4厘米为半径作圆A,点B、C、D中在圆A外的有( )
如图,已知矩形ABCD的边AB=3厘米,AD=4厘米.现以点A为圆心,4厘米为半径作圆A,点B、C、D中在圆A外的有( )| A、0点 | B、1点 | C、2点 | D、3点 |