题目内容
4.阅读下列材料:小明同学遇到下列问题:
解方程组$\left\{{\begin{array}{l}{\frac{2x+3y}{4}+\frac{2x-3y}{3}=7}\\{\frac{2x+3y}{3}+\frac{2x-3y}{2}=8}\end{array}}\right.$,他发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错.如果把方程组中的(2x+3y)看作一个数,把(2x-3y)看作一个数,通过换元,可以解决问题.以下是他的解题过程:
令m=2x+3y,n=2x-3y.
这时原方程组化为$\left\{\begin{array}{l}\frac{m}{4}+\frac{n}{3}=7\\ \frac{m}{3}+\frac{n}{2}=8.\end{array}\right.$解得$\left\{{\begin{array}{l}{m=60}\\{n=-24}\end{array}}\right.$
把$\left\{{\begin{array}{l}{m=60}\\{n=-24}\end{array}}\right.$代入m=2x+3y,n=2x-3y.
得$\left\{{\begin{array}{l}{2x+3y=60}\\{2x-3y=-24}\end{array}}\right.$解得 $\left\{{\begin{array}{l}{x=9}\\{y=14}\end{array}}\right.$
所以,原方程组的解为$\left\{{\begin{array}{l}{x=9}\\{y=14}\end{array}}\right.$
请你参考小明同学的做法,解决下面的问题:
(1)解方程组$\left\{\begin{array}{l}\frac{x+y}{6}+\frac{x-y}{10}=3\\ \frac{x+y}{6}-\frac{x-y}{10}=-1.\end{array}\right.$
(2)若方程组$\left\{\begin{array}{l}{a_1}x+{b_1}y={c_{1,}}\\{a_2}x+{b_2}y={c_{2.}}\end{array}\right.$的解是$\left\{\begin{array}{l}x=3\\ y=2.\end{array}\right.$,求方程组$\left\{\begin{array}{l}\frac{5}{6}{a_1}x+\frac{1}{3}{b_1}y={c_{1,}}\\ \frac{5}{6}{a_2}x+\frac{1}{3}{b_2}y={c_2}.\end{array}\right.$的解.
分析 (1)令m=$\frac{x+y}{6}$,n=$\frac{x-y}{10}$,将方程组整理后,仿照阅读材料中的解法求出解即可;
(2)令m=$\frac{5}{6}$x,n=$\frac{1}{3}$y,将方程组整理后,仿照阅读材料中的解法求出解即可.
解答 解:(1)令m=$\frac{x+y}{6}$,n=$\frac{x-y}{10}$,
原方程组可化为$\left\{\begin{array}{l}m+n=3\\ m-n=-1.\end{array}\right.$,
解得:$\left\{\begin{array}{l}m=1\\ n=2.\end{array}\right.$,
∴$\left\{\begin{array}{l}\frac{x+y}{6}=1\\ \frac{x-y}{10}=2.\end{array}\right.$,
解得$\left\{\begin{array}{l}x=13\\ y=-7.\end{array}\right.$
∴原方程组的解为$\left\{\begin{array}{l}x=13\\ y=-7.\end{array}\right.$;
(2)令m=$\frac{5}{6}$x,n=$\frac{1}{3}$y,
原方程组可化为$\left\{\begin{array}{l}{a_1}m+{b_1}n={c_1}\\{a_2}m+{b_2}n={c_2}.\end{array}\right.$,
依题意,得$\left\{\begin{array}{l}m=3\\ n=2.\end{array}\right.$,
∴$\left\{\begin{array}{l}\frac{5}{6}x=3\\ \frac{1}{3}y=2.\end{array}\right.$,
解得$\left\{\begin{array}{l}x=\frac{18}{5}\\ y=6.\end{array}\right.$.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

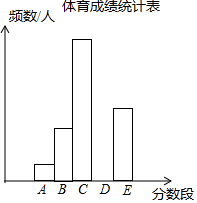 为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如图.
为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如图.| 分数段 | A | B | C | D | E | 合计 |
| 频数/人 | 12 | 36 | 84 | b | 48 | c |
| 频率 | 0.05 | a | 0.35 | 0.25 | 0.20 | 1 |
(1)统计表中,a=0.15,b=60,c=240;将频数分布直方图补充完整.
(2)小明说:“这组数据的众数一定在C中.”你认为小明的说法正确吗?错误(选填“正确”或“错误”).
(3)若成绩在27分及以上定为优秀,则该市30000名九年级学生中体育成绩为优秀的学生人数约有多少?
| A. | 把所有商品逐渐进行检验 | |
| B. | 从中抽取1件进行检验 | |
| C. | 从中挑选几件进行检验 | |
| D. | 从中按抽样规则抽取一定数量的商品进行检验 |
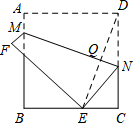 如图,正方形ABCD的边长为4,点M、N分别在AB、CD上.将该纸片沿MN折叠,使点D落在边BC上,设落点为E,折痕MN与DE相交于Q.
如图,正方形ABCD的边长为4,点M、N分别在AB、CD上.将该纸片沿MN折叠,使点D落在边BC上,设落点为E,折痕MN与DE相交于Q.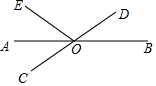 如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC=70°.
如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC=70°.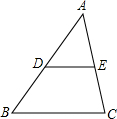 如图,若$\frac{AB}{AD}=\frac{AC}{AE}=\frac{BC}{DE}=\frac{3}{2}$,且△ABC的周长为36cm,则△ADE的周长为24cm.
如图,若$\frac{AB}{AD}=\frac{AC}{AE}=\frac{BC}{DE}=\frac{3}{2}$,且△ABC的周长为36cm,则△ADE的周长为24cm.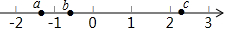 已知实数a,b,c在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-|a+b|+|c+a|+$\sqrt{{(b-c)}^{2}}$-$\root{3}{{c}^{3}}$.
已知实数a,b,c在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-|a+b|+|c+a|+$\sqrt{{(b-c)}^{2}}$-$\root{3}{{c}^{3}}$.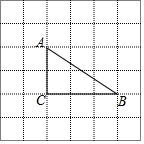 如图,在6×6的网格(小正方形的边长为1)中有一个△ABC,则△ABC的周长是8.606单位长度(精确到0.001)
如图,在6×6的网格(小正方形的边长为1)中有一个△ABC,则△ABC的周长是8.606单位长度(精确到0.001)