题目内容
16.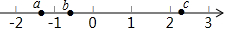 已知实数a,b,c在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-|a+b|+|c+a|+$\sqrt{{(b-c)}^{2}}$-$\root{3}{{c}^{3}}$.
已知实数a,b,c在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-|a+b|+|c+a|+$\sqrt{{(b-c)}^{2}}$-$\root{3}{{c}^{3}}$.
分析 根据图示,可得:-2<a<-1,-1<b<0,2<c<3,据此化简$\sqrt{{a}^{2}}$-|a+b|+|c+a|+$\sqrt{{(b-c)}^{2}}$-$\root{3}{{c}^{3}}$即可.
解答 解:根据图示,可得:-2<a<-1,-1<b<0,2<c<3,
∴a+b<0,c+a>0,b-c<0,
∴$\sqrt{{a}^{2}}$-|a+b|+|c+a|+$\sqrt{{(b-c)}^{2}}$-$\root{3}{{c}^{3}}$
=-a+(a+b)+(c+a)-(b-c)-c
=-a+a+b+c+a-b+c-c
=a+c
点评 此题主要考查了实数的运算,以及数轴的特征和应用,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.

练习册系列答案
相关题目
7.$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$是二元一次方程2x+ay=5的一个解,则a的值为( )
| A. | 1 | B. | $\frac{1}{3}$ | C. | 3 | D. | -1 |
8.下列运算正确的是( )
| A. | a3•a3=2a3 | B. | (a2)3=a6 | C. | 2x+3y=5xy | D. | 2-3=-6 |

 如图,在菱形ABCD中,AB=5,BD=8,点P,Q分别在BD,AD上,则AP+PQ的最小值为$\frac{24}{5}$.
如图,在菱形ABCD中,AB=5,BD=8,点P,Q分别在BD,AD上,则AP+PQ的最小值为$\frac{24}{5}$. 用直尺和圆规作图(不写作法,只保留作图痕迹):
用直尺和圆规作图(不写作法,只保留作图痕迹):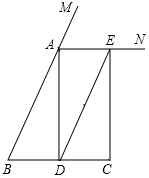 已知:如图,在△ABC中,AB=AC,AD是△ABC的中线,AN为△ABC的外角∠CAM的平分线,CE∥AD,交AN于点E.求证:四边形ADCE是矩形.
已知:如图,在△ABC中,AB=AC,AD是△ABC的中线,AN为△ABC的外角∠CAM的平分线,CE∥AD,交AN于点E.求证:四边形ADCE是矩形.