题目内容
15.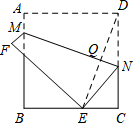 如图,正方形ABCD的边长为4,点M、N分别在AB、CD上.将该纸片沿MN折叠,使点D落在边BC上,设落点为E,折痕MN与DE相交于Q.
如图,正方形ABCD的边长为4,点M、N分别在AB、CD上.将该纸片沿MN折叠,使点D落在边BC上,设落点为E,折痕MN与DE相交于Q.(1)若E是BC的中点,求DN的长;
(2)比较线段DE与MN的大小,并说明理由;
(3)若点G为EF的中点,随着折痕MN位置的变化,请直接写出△GQE周长的最小值.
分析 (1)在Rt△NEC中,利用勾股定理列方程可得DN的长;
(2)如图1,作辅助线,构建直角三角形,证明△MNG≌△DEC(AAS),那么MN=DE.
(3)如图2,取AD的中点P,根据两点之间线段最短得出△GQE周长的最小值.
解答 解:(1)由折叠得:MN是DE的中垂线,
∴DN=EN,
设DN=EN=x,则CN=4-x,
∵E是BC的中点,
∴EC=$\frac{1}{2}$BC=2,
在Rt△NEC中,CN2+CE2=EN2,则(4-x)2+22=x2,
解得:x=2.5,即DN=2.5;
(2)MN=DE,理由是:
如图1,过M点作MG⊥CD,MG交CD于点G,交DE于点H.
由折叠性质可知,DE⊥MN.
∠MHQ+∠HMQ=90°,∠MNG+∠NMG=90°.
则∠MHQ=∠MNG.
又∵MG∥BC.
∴∠MHQ=∠CED.
∴∠MNG=∠DEC.
在△MNG和△DEC中,
∵$\left\{\begin{array}{l}{∠CED=∠GNM}\\{∠C=∠MGN}\\{CD=MG}\end{array}\right.$.
∴△MNG≌△DEC(AAS).
那么MN=DE.
(3)如图2,取AD中点P,连接QP、QG、QC,
由折叠的对称性可知,QP=QG,
∵Q为DE中点,△CDE为直角三角形,
∴CQ=$\frac{1}{2}$DE=QE,
∴△GQE的周长=QG+GE+EQ=2+QP+CQ≥2+CP,
由勾股定理得:CP=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
当且仅当P、Q、C共线时最小,最小为2+2$\sqrt{5}$.
点评 本题考查了折叠的性质、正方形的性质、三角形全等的性质和判定、勾股定理、最值问题,第三问有难度,解题的关键是取AD的中点P,确定QG+QE=QP+QC,属于中考常考题型.

| A. | (5,-1) | B. | (-1,-1) | C. | (5,7) | D. | (-1,7) |
| A. | 1 | B. | $\frac{1}{3}$ | C. | 3 | D. | -1 |
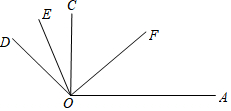 如图所示,已知∠AOE=100°,∠DOF=80°,OE平分∠DOC,OF平分∠AOC,∠EOF=60°.
如图所示,已知∠AOE=100°,∠DOF=80°,OE平分∠DOC,OF平分∠AOC,∠EOF=60°.