题目内容
13．先化简，再求值：（$\frac{{x}^{2}+4}{{x}^{2}-4}$-$\frac{2}{x-2}$）$÷\frac{x}{2}$，其中x=$\sqrt{2}$-2．分析 原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把x的值代入计算即可求出值．
解答 解：原式=$\frac{{x}^{2}+4-2（x+2）}{（x+2）（x-2）}$•$\frac{2}{x}$=$\frac{x（x-2）}{（x+2）（x-2）}$•$\frac{2}{x}$=$\frac{2}{x+2}$，
当x=$\sqrt{2}$-2时，原式=$\sqrt{2}$．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
4．
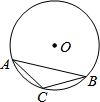如图，△ABC 内接于⊙O，∠A=30°，⊙O的直径为4cm，则点O到BC的距离是（ ）
如图，△ABC 内接于⊙O，∠A=30°，⊙O的直径为4cm，则点O到BC的距离是（ ）| A． | $\sqrt{3}$cm | B． | $\frac{\sqrt{3}}{2}$cm | C． | $\frac{\sqrt{3}}{3}$cm | D． | 2$\sqrt{3}$cm |
1．下列运算中，正确的是（ ）
| A． | 3a+2a2=5a3 | B． | a•a4=a4 | C． | a6÷a3=a2 | D． | （-3x3）2=9x6 |
8．若x=-$\frac{1}{3}$，则|x|的值是（ ）
| A． | 3 | B． | -3 | C． | $\frac{1}{3}$ | D． | -$\frac{1}{3}$ |
18．
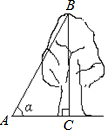如图，在地面上的点A处测得树顶B的仰角为α度，若AC=6米，则树高BC为（ ）
如图，在地面上的点A处测得树顶B的仰角为α度，若AC=6米，则树高BC为（ ）| A． | 6sinα米 | B． | 6tanα米 | C． | $\frac{6}{tanα}$米 | D． | $\frac{6}{cosα}$米 |
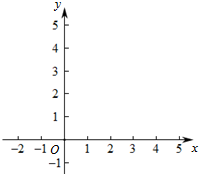在平面直角坐标系xOy中，抛物线y=-$\frac{1}{4}{x^2}$+bx+c经过点A（4，0）和B（0，2）
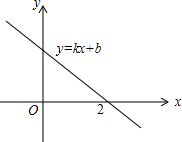如图，一次函数y=kx+b的图象与x轴的交点为（2，0），则下列说法正确的有①②③