题目内容
14.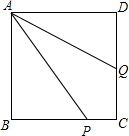 ABCD是正方形,P为BC上任意一点,∠PAD的平分线交CD于Q,求证:DQ=AP-BP.
ABCD是正方形,P为BC上任意一点,∠PAD的平分线交CD于Q,求证:DQ=AP-BP.
分析 首先根据旋转的性质得出∠G=∠AQD,∠GAB=∠QAD,进而得出∠PAG=∠G,即可得出AP=PG=BP+BG=BP+DQ.
解答 解:将△ADQ绕A顺时针旋转90°得到△ABG,由旋转的性质可得出∠G=∠AQD,∠GAB=∠QAB,BG=DQ,
∵AQ平分∠PAD,
∴∠PAQ=∠DAQ,
∴∠PAG=90°-∠PAQ=90°-∠DAQ=∠BAQ,
∵AB∥CD,
∴∠BAQ=∠AQD,
∴∠PAG=∠G,
∴AP=PG=PB+BG=PB+DQ,
即DQ=AP-BP.
点评 此题主要考查了旋转的性质以及角边的关系,根据已知得出PG=BP+BG是解题关键.

练习册系列答案
相关题目
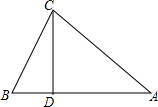 已知:如图.△ABC中,CD⊥AB于D,AC=$\sqrt{34}$cm,BC=$\sqrt{10}$cm,AD=5cm
已知:如图.△ABC中,CD⊥AB于D,AC=$\sqrt{34}$cm,BC=$\sqrt{10}$cm,AD=5cm  已知:如图,∠1和线段m,n.
已知:如图,∠1和线段m,n. 如图,画出⊙O的两条直径,依次连接这两条直径的端点,得一个四边形,判断这个四边形的形状,并说明理由.
如图,画出⊙O的两条直径,依次连接这两条直径的端点,得一个四边形,判断这个四边形的形状,并说明理由. 如图所示,已知AC=BD,CE=DF,AF=BE,求证:AC∥BD,CE∥DF.
如图所示,已知AC=BD,CE=DF,AF=BE,求证:AC∥BD,CE∥DF.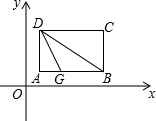 如图,把矩形纸片ABCD置于直角坐标系中,AB∥x轴,BC∥y轴,AB=4,BC=3,点B(5,1)翻折矩形纸片使点A落在对角线DB上的H处得折痕DG.
如图,把矩形纸片ABCD置于直角坐标系中,AB∥x轴,BC∥y轴,AB=4,BC=3,点B(5,1)翻折矩形纸片使点A落在对角线DB上的H处得折痕DG.