题目内容
已知|x-2|+
+z2-6z+9=0，求
•
•
的值．
| 6-y |
| x |
| y |
| z |
考点：配方法的应用,非负数的性质：绝对值,非负数的性质：偶次方,非负数的性质：算术平方根,二次根式的乘除法
专题：计算题
分析：已知等式左边后三项利用完全平方公式变形，利用非负数的性质求出x，y，z的值，代入原式计算即可得到结果．
解答：解：∵|x-2|+
+z2-6z+9=|x-2|+
+（z-3）2=0
∴x-2=0，6-y=0，z-3=0，即x=2，y=6，z=3，
则原式=
×
×
=6．
| 6-y |
| 6-y |
∴x-2=0，6-y=0，z-3=0，即x=2，y=6，z=3，
则原式=
| 2 |
| 6 |
| 3 |
点评：此题考查了配方法的应用，以及非负数的性质，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
相关题目
如图，在?ABCD中，∠ABC=60°，E，F分别在CD，BC的延长线上，AE∥BD，EF⊥BC于点F，DF=2．求EF的长．
如图，某村有一口呈四边形的池塘，在它的四个角A，B，C，D处各栽有一棵大树．该村准备开挖池塘建养鱼池，想使池塘面积扩大一倍，又想保留四棵大树，并要求扩建后的池成平行四边形，请问：村长能否实现这一设想？若能，请你帮村长设计并画出图形；若不能，请说明理由．
如图，E是线段AC上的一点，AB⊥EB于B，AD⊥ED于D，且∠1=∠2，CB=CD，求证：∠3=∠4．
如图所示，在四边形ABCD中，O是AC和BD的交点，点E，F，G，H分别是AO，BO，CO，DO的中点，如果四边形EFGH是平行四边形，那么四边形ABCD也是平行四边形吗？说说你的理由．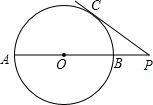
如图，AB是⊙O的直径，P是AB延长线上的一点，PC切⊙O于点C．若PC=6，PB=2，则⊙O的半径是