题目内容
3.已知A=$\root{a-2}{a+b+3}$是a+b+3的算术平方根,B=$\root{a-2b+2}{a+2b}$是a+2b立方根,求B-A的立方根.分析 根据算术平方根和立方根的定义,即可解答.
解答 解:∵A=$\root{a-2}{a+b+3}$是a+b+3的算术平方根,B=$\root{a-2b+2}{a+2b}$是a+2b立方根,
∴a-2=2,a-2b+2=3,
∴a=4,b=2,
∴A=$\root{a-2}{a+b+3}$=$\sqrt{9}$=3,B=$\root{a-2b+2}{a+2b}$=$\root{3}{8}$=2,
∴B-A=2-3=-1,
∴-1的立方根是-1.
点评 本题考查了算术平方根和立方根,解决本题的关键是熟记算术平方根和立方根.

练习册系列答案
相关题目
14.在数轴上表示不等式2x-4>0的解集,正确的是( )
| A. |  | B. |  | C. |  | D. |  |
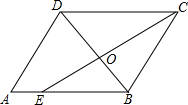 如图.在平行四边形ABCD中,CE是∠OCB的角平分线,且交AB于点E,DB与CE相交于点O,
如图.在平行四边形ABCD中,CE是∠OCB的角平分线,且交AB于点E,DB与CE相交于点O,
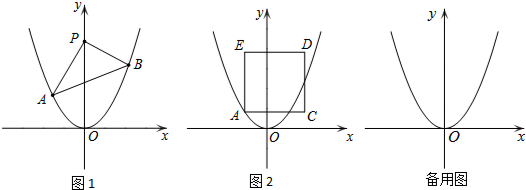
 如图,O是矩形ABCD的交点,DE∥AC,CE∥BD,DE和CE相交于点E,求证:四边形OCED是菱形.
如图,O是矩形ABCD的交点,DE∥AC,CE∥BD,DE和CE相交于点E,求证:四边形OCED是菱形. 如图,在阳光下,身高165cm的小军测得自己的影长为0.9m,同时还测得教学楼的影长为8.1m,求该教学楼的高度.
如图,在阳光下,身高165cm的小军测得自己的影长为0.9m,同时还测得教学楼的影长为8.1m,求该教学楼的高度.