Question

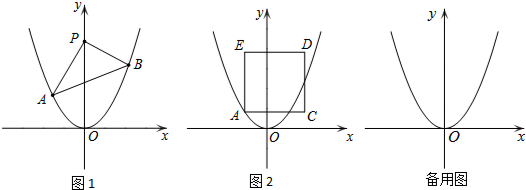
15．如图1，点A，B分别是二次函数y=2x²的图象上的两个点，A、B的横坐标分别为a，b（a＜0，b＞0），点P（0，t）是抛物线对称轴上的任意一点．
（1）当a+b=0时，探究是否存在t，使得△PAB是以AB为底的等腰三角形？若存在，请直接写出t、a、b的其中一组值；若不存在，请说明理由；
（2）当a+b≠0时，探究是否存在t，使得△PAB是以AB为底的等腰三角形？若存在，请写出t的取值范围，并用含t的代数式表示a²+b²的值；若不存在，请说明理由；
（3）如图2作边长为4的正方形ACDE（A、C、D、E按逆时针排列），使得AC∥x轴，若边CD与二次函数的图象总有交点，求a的取值范围．

Answer 1

分析 （1）利用等腰三角形的性质即可；
（2）表示出点的坐标，利用PA=PB建立方程求解即可；
（3）联立方程组求解函数图象的交点坐标．

解答 解：（1）当 a+b=0时，
∴PA=PB∴只需满足t≠2a²即可
∴a=-1，b=1，t=3，
（2）∵A（a，2a²），B（b，2b²），P（0，t）
∵PA=PB，
∴a²+（t-2a²）²=b²+（t-2b²）²
∴a²-b²+（t-2a²）²-（t-2b²）²=0，
（a²-b²）[1-4（t-a²-b²）]=0，
∵a²-b²≠0
∴1-4（t-a²-b²）=0
∴a²+b²=t-$\frac{1}{4}$，
∴t-$\frac{1}{4}$＞0，
∴t＞$\frac{1}{4}$，
（3）A（a，2a²），
∴C（a+4，2a²） D（a+4，2a²+4），
设边CD与二次函数图象交点为F（a+4，2（a+4）²）
由题意可得：$\left\{\begin{array}{l}2{（a+4）^2}≥2{a^2}\\ 2{a^2}+4≥2{（a+4）^2}\end{array}\right.$
∴$\left\{\begin{array}{l}a≥-2\\ a≤-\frac{7}{4}\end{array}\right.$
∴$-2≤a≤-\frac{7}{4}$，

点评 此题是二次函数综合题，主要考查了二次函数的性质，求交点坐标的方法，非负性的考查，解本题的关键是点的坐标的表示．