题目内容
 如图,在正方形ABCD的外侧,作等边△ADE,则∠BED=
如图,在正方形ABCD的外侧,作等边△ADE,则∠BED=考点:正方形的性质,等边三角形的性质
专题:
分析:根据正方形的性质,可得AB与AD的关系,∠BAD的度数,根据等边三角形的性质,可得AE与AD的关系,∠AED的度数,根据等腰三角形的性质,可得∠AEB与∠ABE的关系,根据三角形的内角和,可得∠AEB的度数,根据角的和差,可得答案.
解答:解:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°.
∵等边三角形ADE,
∴AD=AE,∠DAE=∠AED=60°.
∠BAE=∠BAD+∠DAE=90°+60°=150°,
AB=AE,
∠AEB=∠ABE=(180°-∠BAE)÷2=15°,
∠BED=∠DAE-∠AEB=60°-15°=45°,
故答案为:45°.
∴AB=AD,∠BAD=90°.
∵等边三角形ADE,
∴AD=AE,∠DAE=∠AED=60°.
∠BAE=∠BAD+∠DAE=90°+60°=150°,
AB=AE,
∠AEB=∠ABE=(180°-∠BAE)÷2=15°,
∠BED=∠DAE-∠AEB=60°-15°=45°,
故答案为:45°.
点评:本题考查了正方形的性质,先求出∠BAE的度数,再求出∠AEB,最后求出答案.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
如图,这是由边长为1的正六边形摆出的一系列图形,按这种方式摆下去,则第10个图形的周长是( )


| A、55 | B、60 | C、65 | D、70 |
 如图,直线l1:y=ax+2与y轴相交于点E,已知A(-2,1),B(-2,-1),C(1,-1)且ABCD是矩形,设l2过点E,且l1⊥l2,
如图,直线l1:y=ax+2与y轴相交于点E,已知A(-2,1),B(-2,-1),C(1,-1)且ABCD是矩形,设l2过点E,且l1⊥l2, 如图,以矩形OABC的顶点O为原点,OA为x轴,OC为y轴建立平面直角坐标系,双曲线
如图,以矩形OABC的顶点O为原点,OA为x轴,OC为y轴建立平面直角坐标系,双曲线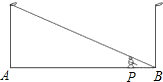 如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触路灯B的底部,这时他离路灯A有20米,离路灯B有5米,如果小亮的身高为1.6米,那么路灯高度为
如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触路灯B的底部,这时他离路灯A有20米,离路灯B有5米,如果小亮的身高为1.6米,那么路灯高度为 如图,平行四边形ABCD中,M,N分别是AB,CD的中点,将四边形MBCN沿直线MN折叠后得到四边形MB′C′N,MB′与DN交于点P.若∠A=64°,则∠MPN=
如图,平行四边形ABCD中,M,N分别是AB,CD的中点,将四边形MBCN沿直线MN折叠后得到四边形MB′C′N,MB′与DN交于点P.若∠A=64°,则∠MPN= 如图,在矩形ABCD中,AD=3,BD=5,则此矩形的周长为
如图,在矩形ABCD中,AD=3,BD=5,则此矩形的周长为