题目内容
 如图,以矩形OABC的顶点O为原点,OA为x轴,OC为y轴建立平面直角坐标系,双曲线y=
如图,以矩形OABC的顶点O为原点,OA为x轴,OC为y轴建立平面直角坐标系,双曲线y=| k |
| x |
考点:反比例函数综合题
专题:综合题
分析:根据AB:BC=2:3,设AB=2t,BC=3t,表示出A,B的坐标,根据D、E分别为反比例函数与BC、AB的交点,得出D与E坐标,根据直线DE将△DBE翻折得△DFE,且点F恰好落在直线OA上,得到BF垂直于DE,且BF中点在DE上,表示出DE的斜率,进而确定出直线DE方程,利用两直线垂直时斜率乘积为-1得出直线BF斜率,表示出直线BF方程,进而表示出F坐标,利用中点坐标公式表示出BF中点坐标,代入直线DE中整理表示出t2,即可确定出矩形的面积.
解答:解:根据AB:BC=2:3,设AB=2t,则有BC=3t,即A(3t,0),B(3t,2t),
∵E、D为反比例函数y=
与BC、BA的交点,
∴D(3t,
),E(
,2t),
∵直线DE将△DBE翻折得△DFE,且点F恰好落在直线OA上,
∴BF⊥DE,BF的中点在DE上,
∵直线DE的斜率为
=-
,方程为y-2t=-
(x-
),
∴直线BF斜率为
,
∴直线BF解析式为y-2t=
(x-3t),即y=
x-
t,
令y=0,得到x=
t,即F(
t,0),
∴BF的中点坐标为(
,t),
将中点坐标代入直线DE解析式得:t-2t=-
(
t-
),
整理得:t2=
k,
则S矩形=3t•2t=6t2=
k.
故答案为:
k
∵E、D为反比例函数y=
| k |
| x |
∴D(3t,
| k |
| 3t |
| k |
| 2t |
∵直线DE将△DBE翻折得△DFE,且点F恰好落在直线OA上,
∴BF⊥DE,BF的中点在DE上,
∵直线DE的斜率为
2t-
| ||
|
| 2 |
| 3 |
| 2 |
| 3 |
| k |
| 2t |
∴直线BF斜率为
| 3 |
| 2 |
∴直线BF解析式为y-2t=
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
令y=0,得到x=
| 5 |
| 3 |
| 5 |
| 3 |
∴BF的中点坐标为(
3t+
| ||
| 2 |
将中点坐标代入直线DE解析式得:t-2t=-
| 2 |
| 3 |
| 7 |
| 3 |
| k |
| 2t |
整理得:t2=
| 3 |
| 5 |
则S矩形=3t•2t=6t2=
| 18 |
| 5 |
故答案为:
| 18 |
| 5 |
点评:此题属于反比例函数综合题,涉及的知识有:坐标与图形性质,两直线垂直时斜率满足的关系,直线的点斜式方程,线段中点坐标公式,以及对称的性质,熟练掌握反比例函数的性质是解本题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
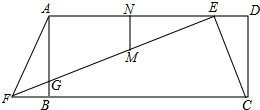 如图,在矩形ABCD中,点E是AD边上一点,点F是CB延长线上一点,连接EF交AB于点G,且DE=BF.AE的垂直平分线MN交AE于点N、交EF于点M.若∠AFG=2∠BFG=45°,AF=2.
如图,在矩形ABCD中,点E是AD边上一点,点F是CB延长线上一点,连接EF交AB于点G,且DE=BF.AE的垂直平分线MN交AE于点N、交EF于点M.若∠AFG=2∠BFG=45°,AF=2.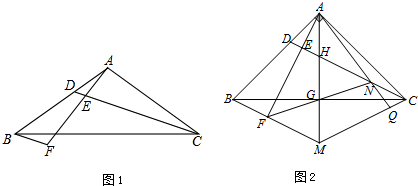
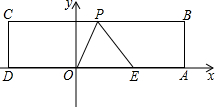 如图,在平面直角坐标系中,O为坐标原点,四边形ABCD是矩形,顶点A、B、C、D的坐标分别为(7,0),(7,4),(-4,4),(-4,0),点E(5,0),点P在CB边上运动,使△OPE为等腰三角形,则满足条件的点P有
如图,在平面直角坐标系中,O为坐标原点,四边形ABCD是矩形,顶点A、B、C、D的坐标分别为(7,0),(7,4),(-4,4),(-4,0),点E(5,0),点P在CB边上运动,使△OPE为等腰三角形,则满足条件的点P有 如图,在正方形ABCD的外侧,作等边△ADE,则∠BED=
如图,在正方形ABCD的外侧,作等边△ADE,则∠BED=