题目内容
 如图,平行四边形ABCD中,M,N分别是AB,CD的中点,将四边形MBCN沿直线MN折叠后得到四边形MB′C′N,MB′与DN交于点P.若∠A=64°,则∠MPN=
如图,平行四边形ABCD中,M,N分别是AB,CD的中点,将四边形MBCN沿直线MN折叠后得到四边形MB′C′N,MB′与DN交于点P.若∠A=64°,则∠MPN=考点:翻折变换(折叠问题),平行四边形的性质
专题:
分析:根据平行四边形的性质求出∠BMN的度数,根据折叠的性质求出∠NMP的度数,再根据平角的定义得到∠AMP的度数,再根据平行线的性质即可求解.
解答:解:(1)∵四边形ABCD是平行四边形,M,N分别是AB,CD的中点,
∴AB∥CD,AD∥MN.
∴∠BMN=∠A=64°,
由折叠的性质可得∠NMP=64°,
∴∠AMP=180°-64°×2=52°,
∴∠MPN=52°.
故答案为:52.
∴AB∥CD,AD∥MN.
∴∠BMN=∠A=64°,
由折叠的性质可得∠NMP=64°,
∴∠AMP=180°-64°×2=52°,
∴∠MPN=52°.
故答案为:52.
点评:本题考查了翻折变换(折叠问题),平行四边形的性质,平角的定义和平行线的性质,综合性较强,难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在Rt△ABC中,∠C=90°,AC=3,AB=5,那么sinA的值是( )
在Rt△ABC中,∠C=90°,AC=3,AB=5,那么sinA的值是( )A、
| ||
B、
| ||
C、
| ||
D、
|
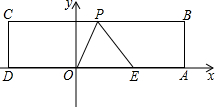 如图,在平面直角坐标系中,O为坐标原点,四边形ABCD是矩形,顶点A、B、C、D的坐标分别为(7,0),(7,4),(-4,4),(-4,0),点E(5,0),点P在CB边上运动,使△OPE为等腰三角形,则满足条件的点P有
如图,在平面直角坐标系中,O为坐标原点,四边形ABCD是矩形,顶点A、B、C、D的坐标分别为(7,0),(7,4),(-4,4),(-4,0),点E(5,0),点P在CB边上运动,使△OPE为等腰三角形,则满足条件的点P有 如图,在正方形ABCD的外侧,作等边△ADE,则∠BED=
如图,在正方形ABCD的外侧,作等边△ADE,则∠BED= 如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD,CD=
如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD,CD= 如图,线段AD与BC相交于点O,连结AB、CD,且∠B=∠D,要使△AOB≌△COD,应添加一个条件是
如图,线段AD与BC相交于点O,连结AB、CD,且∠B=∠D,要使△AOB≌△COD,应添加一个条件是