题目内容
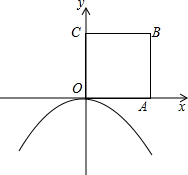 如图,边长为1的正方形OABC的顶点A在x轴的正半轴上.将正方形OABC绕点O顺时针旋转30°,点A恰好落在开口向下的抛物线y=ax2上.
如图,边长为1的正方形OABC的顶点A在x轴的正半轴上.将正方形OABC绕点O顺时针旋转30°,点A恰好落在开口向下的抛物线y=ax2上.(1)求出抛物线的解析式;
(2)将正方形继续旋转多少度时,可以使点A再次落在此抛物线上?
考点:正方形的性质,二次函数图象上点的坐标特征,坐标与图形变化-旋转
专题:
分析:(1)设旋转后的点A的对应点为A′,作A′D⊥x轴于D,根据直角三角形30°角所对的直角边等于斜边的一半求出A′D,再利用勾股定理列式求出OD,从而得到点A′的坐标,再利用待定系数法求一次函数解析式解答;
(2)根据抛物线的对称性,点A再次落在抛物线上时OA与x轴负半轴的夹角为30°,然后求解即可.
(2)根据抛物线的对称性,点A再次落在抛物线上时OA与x轴负半轴的夹角为30°,然后求解即可.
解答: 解:(1)如图,设旋转后的点A的对应点为A′,作A′D⊥x轴于D,
解:(1)如图,设旋转后的点A的对应点为A′,作A′D⊥x轴于D,
∵旋转角为30°,
∴∠A′OD=30°,
∴A′D=
OA′=
,
由勾股定理得,OD=
=
,
∴点A′(
,-
),
∴a(
)2=-
,
解得a=-
,
∴抛物线解析式为y=-
x2;
(2)∵抛物线y=-
x2的对称轴为y轴,
∴点A再次落在抛物线上时OA与x轴负半轴的夹角为30°,
∵180°-30°×2=120°,
∴正方形继续旋转120°.
 解:(1)如图,设旋转后的点A的对应点为A′,作A′D⊥x轴于D,
解:(1)如图,设旋转后的点A的对应点为A′,作A′D⊥x轴于D,∵旋转角为30°,
∴∠A′OD=30°,
∴A′D=
| 1 |
| 2 |
| 1 |
| 2 |
由勾股定理得,OD=
12-(
|
| ||
| 2 |
∴点A′(
| ||
| 2 |
| 1 |
| 2 |
∴a(
| ||
| 2 |
| 1 |
| 2 |
解得a=-
| 2 |
| 3 |
∴抛物线解析式为y=-
| 2 |
| 3 |
(2)∵抛物线y=-
| 2 |
| 3 |
∴点A再次落在抛物线上时OA与x轴负半轴的夹角为30°,
∵180°-30°×2=120°,
∴正方形继续旋转120°.
点评:本题考查了正方形性质,待定系数法求二次函数解析式,二次函数图象上点的坐标特征,坐标与图形变化-旋转,熟记各性质并求出旋转后点A的对应点的坐标是解题的关键.

练习册系列答案
相关题目
 如图,已知DE、BF分别垂直于AC于E、F,且DE=BF,AE=CF.
如图,已知DE、BF分别垂直于AC于E、F,且DE=BF,AE=CF.