题目内容
 如图,已知DE、BF分别垂直于AC于E、F,且DE=BF,AE=CF.
如图,已知DE、BF分别垂直于AC于E、F,且DE=BF,AE=CF.求证:四边形ABCD是平行四边形.
考点:平行四边形的判定,全等三角形的判定与性质
专题:证明题
分析:首先根据DE、BF分别垂直于AC于E、F,得到∠AED=∠CFB=90°,利用SAS证得△ADE≌△CBF,从而证得AD∥BC,利用一组对边平行且相等的四边形是平行四边形判定四边形ABCD是平行四边形.
解答:证明:∵DE、BF分别垂直于AC于E、F,
∴∠AED=∠CFB=90°,
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS),
∴AD=BC,∠DAE=∠BCF,
∴AD∥BC
∴四边形ABCD是平行四边形.
∴∠AED=∠CFB=90°,
在△ADE和△CBF中,
|
∴△ADE≌△CBF(SAS),
∴AD=BC,∠DAE=∠BCF,
∴AD∥BC
∴四边形ABCD是平行四边形.
点评:考查了平行四边形的判定,解题的关键是牢记平行四边形的判定方法,难度中等.

练习册系列答案
相关题目
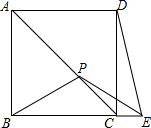 如图,正方形ABCD中,P是AC上一点,E是BC延长线上一点,且PB=PE.若BP=PE=
如图,正方形ABCD中,P是AC上一点,E是BC延长线上一点,且PB=PE.若BP=PE=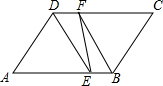 如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于E,BF平分∠ABC交CD于F.
如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于E,BF平分∠ABC交CD于F.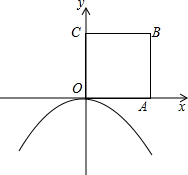 如图,边长为1的正方形OABC的顶点A在x轴的正半轴上.将正方形OABC绕点O顺时针旋转30°,点A恰好落在开口向下的抛物线y=ax2上.
如图,边长为1的正方形OABC的顶点A在x轴的正半轴上.将正方形OABC绕点O顺时针旋转30°,点A恰好落在开口向下的抛物线y=ax2上.