题目内容
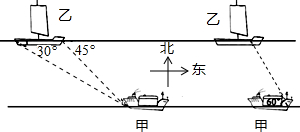
甲、乙两船分别在相距120米的两平行航线上向东匀速行驶,小明站在甲船的船尾对着乙船拍照,此时他发现乙船的船尾在他们的西偏北30°方向,船头在他的西偏北45°方向.小明迅速用30秒时间走向船头,此时发现乙船船头在他的西偏北60°方向.已知甲船长20米,甲船的速度为600米/分.求乙船的长度和乙船的速度.(结果取整数)(参考数据:
≈1.73)
| 3 |

考点:解直角三角形的应用-方向角问题
专题:
分析:设甲船头为A,船尾为B,乙船头为D,船尾为C.过B作BH⊥CD于H.先解直角△BDH与直角△BCH,求出DH=120米,CH=120
米,则乙船长度CD=(120
-120)≈88米.再过A′作A′E⊥CD于E,由A′E=120米,得出D′E=40
米.又AA′=600×
=300(米),则HE=BA′=320米,乙船从D到D′走了(440-40
)米,用时30秒=
分,然后根据速度=路程÷时间即可求解.
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
解答: 解:如图,设甲船头为A,船尾为B,乙船头为D,船尾为C.过B作BH⊥CD于H.
解:如图,设甲船头为A,船尾为B,乙船头为D,船尾为C.过B作BH⊥CD于H.
∵BH=120米,
∴DH=120米,CH=120
米,
∴乙船长度CD=(120
-120)≈88米.
同理过A′作A′E⊥CD于E,A′E=120米,
∴D′E=40
米.
又∵AA′=600×
=300(米),
∴HE=BA′=320米,
∴乙船从D到D′走了(440-40
)米,用时30秒=
分,
∴乙船速度为(440-40
)÷
=(880-80
)≈742米/分.
答:乙船长度约为88米,乙船的速度约为742米/分.
 解:如图,设甲船头为A,船尾为B,乙船头为D,船尾为C.过B作BH⊥CD于H.
解:如图,设甲船头为A,船尾为B,乙船头为D,船尾为C.过B作BH⊥CD于H.∵BH=120米,
∴DH=120米,CH=120
| 3 |
∴乙船长度CD=(120
| 3 |
同理过A′作A′E⊥CD于E,A′E=120米,
∴D′E=40
| 3 |
又∵AA′=600×
| 1 |
| 2 |
∴HE=BA′=320米,
∴乙船从D到D′走了(440-40
| 3 |
| 1 |
| 2 |
∴乙船速度为(440-40
| 3 |
| 1 |
| 2 |
| 3 |
答:乙船长度约为88米,乙船的速度约为742米/分.
点评:本题考查了解直角三角形的应用-方向角问题,有一定难度.准确作出辅助线构造直角三角形是解题的关键.

练习册系列答案
相关题目
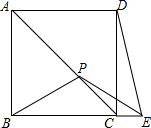 如图,正方形ABCD中,P是AC上一点,E是BC延长线上一点,且PB=PE.若BP=PE=
如图,正方形ABCD中,P是AC上一点,E是BC延长线上一点,且PB=PE.若BP=PE=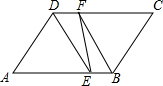 如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于E,BF平分∠ABC交CD于F.
如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于E,BF平分∠ABC交CD于F. 如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,在A处有一所中学,AP=160米,拖拉机在公路MN上沿PN方向以每秒5米的速度行驶,假设拖拉机行驶时周围100米以内有噪音影响.
如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,在A处有一所中学,AP=160米,拖拉机在公路MN上沿PN方向以每秒5米的速度行驶,假设拖拉机行驶时周围100米以内有噪音影响.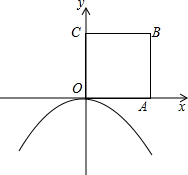 如图,边长为1的正方形OABC的顶点A在x轴的正半轴上.将正方形OABC绕点O顺时针旋转30°,点A恰好落在开口向下的抛物线y=ax2上.
如图,边长为1的正方形OABC的顶点A在x轴的正半轴上.将正方形OABC绕点O顺时针旋转30°,点A恰好落在开口向下的抛物线y=ax2上.