题目内容
一个不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(除颜色外其余都相同),其中红球2个(分别标有1号、2号),蓝球1个,黄球1个.
(1)若从中任意摸出一个球,它是蓝球的概率为多少?
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用画树状图或列表格的方法,求两次摸到不同颜色球的概率.
(1)若从中任意摸出一个球,它是蓝球的概率为多少?
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用画树状图或列表格的方法,求两次摸到不同颜色球的概率.
考点:列表法与树状图法
专题:计算题
分析:(1)找出4个小球中蓝球的个数,即可确定出概率;
(2)列表得出所有等可能的情况数,找出两次摸到不同颜色球的情况,即可求出所求的概率.
(2)列表得出所有等可能的情况数,找出两次摸到不同颜色球的情况,即可求出所求的概率.
解答:解:(1)4个小球中蓝球有1个,
则P(取出是蓝球)=
;
(2)列表如下:
所有等可能的情况有12种,其中两次摸到不同颜色球的情况有10种,
则P=
=
.
则P(取出是蓝球)=
| 1 |
| 4 |
(2)列表如下:
| 红1 | 红2 | 黄 | 蓝 | |
| 红1 | --- | (红1,红2) | (红1,黄) | (红1,蓝) |
| 红2 | (红2,红1) | --- | (红2,黄) | (红2,蓝) |
| 黄 | (黄,红1) | (黄,红2) | --- | (黄,蓝) |
| 蓝 | (蓝,红1) | (蓝,红2) | (蓝,黄) | --- |
则P=
| 10 |
| 12 |
| 5 |
| 6 |
点评:此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
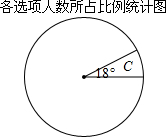 (1)在一次考试中,李老师从所教两个班全体参加考试的80名学生中随机抽取了20名学生的答题卷进行统计分析.其中某个单项选择题答题情况如下表(没有多选和不选):
(1)在一次考试中,李老师从所教两个班全体参加考试的80名学生中随机抽取了20名学生的答题卷进行统计分析.其中某个单项选择题答题情况如下表(没有多选和不选):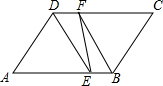 如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于E,BF平分∠ABC交CD于F.
如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于E,BF平分∠ABC交CD于F.
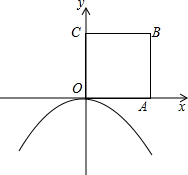 如图,边长为1的正方形OABC的顶点A在x轴的正半轴上.将正方形OABC绕点O顺时针旋转30°,点A恰好落在开口向下的抛物线y=ax2上.
如图,边长为1的正方形OABC的顶点A在x轴的正半轴上.将正方形OABC绕点O顺时针旋转30°,点A恰好落在开口向下的抛物线y=ax2上. 如图,Rt△ABC,∠BAC=90°,分别以AB、AC为边向三角形外作两个正方形,如图所示,其中两个正方形的面积是6和3,则斜边BC=
如图,Rt△ABC,∠BAC=90°,分别以AB、AC为边向三角形外作两个正方形,如图所示,其中两个正方形的面积是6和3,则斜边BC=