题目内容
19.一元二次方程-3x2=5(x-3)的二次项系数是3,常数项是-15.分析 方程整理为一般形式,找出二次项系数,常数项即可.
解答 解:方程整理得:3x2+5x-15=0,
则方程的二次项系数为3,常数项为-15,
故答案为:3;-15
点评 此题考查了一元二次方程的一般形式,一元二次方程的一般形式是:ax2+bx+c=0(a,b,c是常数且a≠0)特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.在一般形式中ax2叫二次项,bx叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
9.若两个非零有理数a,b,满足|a|=a,|b|=-b,a+b<0,则a,b的取值符合题意的是( )
| A. | a=2,b=-1 | B. | a=-2,b=1 | C. | a=1,b=-2 | D. | a=-1,b=-2 |
10.下列实数中,是无理数的是( )
| A. | $\frac{11}{7}$ | B. | 0.1010010001 | C. | $\root{3}{9}$ | D. | 0 |
7.下列说法错误的是( )
| A. | 48°21′36″的余角是41.64° | |
| B. | 点C是线段AB上的点,AB=10,AC=6,点D是线段BC的中点,则线段CD=2 | |
| C. | ∠AOC=60°,经过顶点O引一条射线OD,且∠AOD=25°,则∠COD=85° | |
| D. | 已知线段a,b如图 ,则尺规作图中 ,则尺规作图中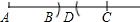 ,线段AD=2a-b ,线段AD=2a-b |
4.顺次连接四边形ABCD各边的中点,所得四边形是( )
| A. | 平行四边形 | B. | 对角线互相垂直的四边形 | ||
| C. | 矩形 | D. | 菱形 |
11.已知点P(2+m,n-3)与点Q(m,1+n)关于原点对称,则m-n的值是( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
7. 如图,?ABCD中,E、F是边BC的三等分点,AF交DE于点M,则AM:AF等于( )
如图,?ABCD中,E、F是边BC的三等分点,AF交DE于点M,则AM:AF等于( )
 如图,?ABCD中,E、F是边BC的三等分点,AF交DE于点M,则AM:AF等于( )
如图,?ABCD中,E、F是边BC的三等分点,AF交DE于点M,则AM:AF等于( )| A. | 3:2 | B. | 2:3 | C. | 3:4 | D. | 4:3 |
 已知:抛物线y=-x2-2x+3与x轴相交于A、B两点(点A在点B左侧),与y轴交于点C,顶点为P.
已知:抛物线y=-x2-2x+3与x轴相交于A、B两点(点A在点B左侧),与y轴交于点C,顶点为P.