Question

6．已知：抛物线y=-x²-2x+3与x轴相交于A、B两点（点A在点B左侧），与y轴交于点C，顶点为P．
（1）求A、B、P三点的坐标；
（2）在直角坐标系内画出抛物线简图，求出S_△ACP；
（3）已知点M是抛物线上的一个动点，且在第二象限内，当△ACM的面积最大时，求出此时点M的坐标和△ACM的最大面积．

Answer 1

分析 （1）根据与x轴的交点坐标即y=0时，求出x的值，根据顶点式求出顶点坐标，即可解答；
（2）画出图形，根据S_△ACP=S_{长方形AOEF}-S_△AOC-S_△PEC-S_△AFP，即可解答；
（3）由函数的解析式画出大致图象，当-2＜x＜0或-3＜x≤-2时，如图1、2，设△ACM的面积为S，M（x，-x²-2x+3）（x＜0），作ME⊥y轴，就有ME=-x，OE=-x²-2x+3，由三角形的面积公式和梯形的面积公式就可以求出结论．

解答 解：（1）当y=0时，-x²-2x+3=0，
解得：x₁=-3，x₂=1，
∵点A在点B左侧，
∴点A（-3，0），点B（1，0），
当x=0时，y=3，
∴点C的坐标为（0，3），
∵y=-x²-2x+3=-（x+1）²+4，
∴点P的坐标为（-1，4）；
（2）如图1，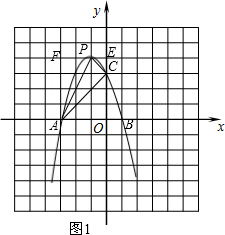

∵点A（-3，0），点B（1，0），点P的坐标为（-1，4），
∴AO=3，OC=3，OP=4，
∴S_△ACP=S_{长方形AOEF}-S_△AOC-S_△PEC-S_△AFP
=3×4-$\frac{1}{2}$×3×3-$\frac{1}{2}$×1×1-$\frac{1}{2}$×4×2
=3．
（3）设△ACM的面积为S，M（x，-x²-2x+3）（x＜0），作ME⊥y轴
∴ME=-x，OE=-x²-2x+3．
∵y=-x²-2x+3，
∴y=0时，0=-x²-2x+3，
∴x₁=1，x₂=-3．
∵点A在点B左侧，
∴OA=3．
如图2，当-2＜x＜0时，

S₁=$\frac{（-x+3）（-{x}^{2}-2x+3）}{2}$-$\frac{（-{x}^{2}-2x+3-3）（-x）}{2}$-4.5，
=-$\frac{3}{2}$x²-$\frac{9}{2}$x，
=-$\frac{3}{2}$（x+$\frac{3}{2}$）²+$\frac{27}{8}$，
∴a=-$\frac{3}{2}$＜0，抛物线开口向下，函数有最大值．
∴x=-$\frac{3}{2}$时，S_最大=$\frac{27}{8}$；
∵-2＜x＜0，
x=-2时，S_最大=3
如图3，当-3＜x≤-2时，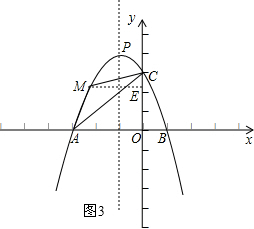

S₂=$\frac{（-x+3）（-{x}^{2}-2x+3）}{2}$+$\frac{-x（3+{x}^{2}+2x-3）}{2}$-$\frac{9}{2}$，
=-$\frac{3}{2}$x²-$\frac{9}{2}$x，
=-$\frac{3}{2}$（x+$\frac{3}{2}$）²+$\frac{27}{8}$，
∴a=-$\frac{3}{2}$＜0，
∴抛物线的开口向下，在对称轴的左侧S随x的增大而增大．
∴x=-2时，S_最大=3
∵$\frac{27}{8}$＞3，
∴x=-$\frac{3}{2}$时，S_△ACM最大=$\frac{27}{8}$．
∴M（-$\frac{3}{2}$，$\frac{15}{4}$）．
答：M（-$\frac{3}{2}$，$\frac{15}{4}$）时，S_△ACM最大=$\frac{27}{8}$．

点评 本题考查了二次函数的图象的性质的运用，三角形的面积公式的运用，梯形的面积公式的运用，抛物线与x轴的交点坐标的运用，分类讨论的运用．解答时求出S与x的关系式是关键．