题目内容
5．
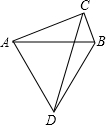如图，以线段AB为边分别作直角三角形ABC和等边三角形ABD，其中∠ACB=90°．连接CD，当CD的长度最大时，此时∠CAB的大小是（ ）| A． | 75° | B． | 45° | C． | 30° | D． | 15° |
分析 利用圆周角定理结合点到直线的距离得出C′在半圆的中点时，此时当CD的长度最大，进而得出答案．
解答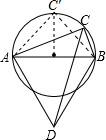 
解：如图所示：
∵AB长一定，
∴只有C点距离AB距离最大，则CD的长度最大，
∴只有C点在C′位置，即C′在半圆的中点时，此时当CD的长度最大，
故此时AC′=BC′，
∴∠C′AB的大小是45°．
故选：B．
点评 此题主要考查了圆周角定理以及点到直线的距离，得出C点位置是解题关键．
练习册系列答案
相关题目
15．下列不是同类项的是（ ）
| A． | 0与$\frac{1}{2}$ | B． | 5x与2y | C． | -$\frac{1}{4}$a2b与3a2b | D． | -2x2y2与$\frac{1}{2}$x2y2 |
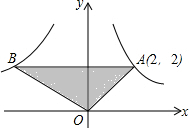如图，点A（2，2）是反比例函数y=$\frac{m}{x}$（x＞0）的图象上一点，点B是反比例函数y=$\frac{n}{x}$（x＜0）上一点，AB与x轴平行，且△OAB的面积为5，则m+n=-2．
20．下列图案中，既是中心对称图形，又是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
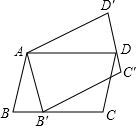如图，将?ABCD绕点A逆时针旋转30°得到?AB′C′D′，点B′恰好落在BC边上，则∠DAB′=75°．
17．正比例函数y=（2k+1）x，若y随x增大而减小，则k的取值范围是（ ）
| A． | k＞-$\frac{1}{2}$ | B． | k＜-$\frac{1}{2}$ | C． | k=$\frac{1}{2}$ | D． | k=0 |
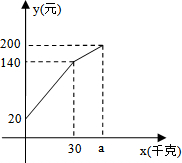一农民带上若干千克自产的西红柿进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售，售出的西红柿千克数x与他手中持有的钱数y（含备用零钱）的关系，如图所示，结合图象回答下列问题．