题目内容
15.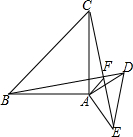 如图,AB=AC,AD=AE,∠BAC=∠DAE=90°.
如图,AB=AC,AD=AE,∠BAC=∠DAE=90°.(1)求证:△ABD≌△ACE;
(2)求证:CE⊥BD;
(3)求∠AFB的度数.
分析 (1)先证出∠BAD=∠CAE,由SAS证明△ABD≌△ACE即可;
(2)由全等三角形的性质得出∠ABD=∠ACE,由角的互余关系和对顶角相等得出∠ACE+∠CGF=90°,得出∠BFC=90°即可;
(3)证明A、B、C、F四点共圆,由圆周角定理得出∠AFB=∠ACB=45°即可.
解答 (1)证明:∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,$\left\{\begin{array}{l}{AB=AC}&{\;}\\{∠BAD=∠CAE}&{\;}\\{AD=AE}&{\;}\end{array}\right.$,
∴△ABD≌△ACE(SAS);
(2)证明:如图所示: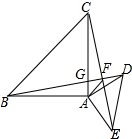
∵△ABD≌△ACE,
∴∠ABD=∠ACE,
∵∠BAC=90°,
∴∠ABD+∠AGB=90°,
∵∠AGB=∠CGF,
∴∠ACE+∠CGF=90°,
∴∠BFC=90°,
∴CE⊥BD;
(3)解:∵∠BAC=90°,AB=AC,∠BFC=90°,
∴A、B、C、F四点共圆,∠ACB=45°,
∴∠AFB=∠ACB=45°.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形的性质、四点共圆、圆周角定理;熟练掌握全等三角形的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
20.抛物线y=$\frac{1}{2}{x}^{2}$与y=-$\frac{1}{2}{x}^{2}$的位置关系是( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | ||
| C. | 关于直线y=x轴对称 | D. | 关于直线y=-x对称 |
7.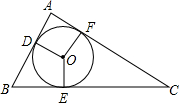 如图,⊙O是△ABC的内切圆.切点分别为D、E、F,若∠DOE=120°,∠EOF=150°,则△ABC的3个内角的度数依次为( )
如图,⊙O是△ABC的内切圆.切点分别为D、E、F,若∠DOE=120°,∠EOF=150°,则△ABC的3个内角的度数依次为( )
 如图,⊙O是△ABC的内切圆.切点分别为D、E、F,若∠DOE=120°,∠EOF=150°,则△ABC的3个内角的度数依次为( )
如图,⊙O是△ABC的内切圆.切点分别为D、E、F,若∠DOE=120°,∠EOF=150°,则△ABC的3个内角的度数依次为( )| A. | 90°,60°,30° | B. | 80°,60°,40° | C. | 90°,50°,40° | D. | 80°,70°,30° |
16. 如图,直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,当△ABC和△APQ全等时,AP长度为( )
如图,直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,当△ABC和△APQ全等时,AP长度为( )
 如图,直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,当△ABC和△APQ全等时,AP长度为( )
如图,直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,当△ABC和△APQ全等时,AP长度为( )| A. | 5cm | B. | 10cm | C. | 5cm或10cm | D. | 不存在 |
 已知如图:AE=DB,∠C=∠F,BC∥EF.求证:AC∥DF.
已知如图:AE=DB,∠C=∠F,BC∥EF.求证:AC∥DF. 如图,DE∥BC,S△DOE:S△COB=4:9,求AD:BD.
如图,DE∥BC,S△DOE:S△COB=4:9,求AD:BD. 如图所示,图中线段有多少条?请分别写出来.
如图所示,图中线段有多少条?请分别写出来.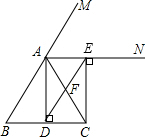 如图,在△ABC中,AB=AC,AD⊥BC垂足为D,AN平分∠CAM,CE⊥AN垂足为E,连接DE交AC于F.
如图,在△ABC中,AB=AC,AD⊥BC垂足为D,AN平分∠CAM,CE⊥AN垂足为E,连接DE交AC于F.