题目内容
6. 如图,DE∥BC,S△DOE:S△COB=4:9,求AD:BD.
如图,DE∥BC,S△DOE:S△COB=4:9,求AD:BD.
分析 根据DE∥BC,即可求得△ADE∽△ABC,根据三角形面积计算公式和相似三角形对应边比值相等的性质可以求得AD:AB,即可求得AD:DB,即可解题.
解答 解:∵DE∥BC,
∴△DOE∽△COB,
∴S△DOE:S△COB=($\frac{DE}{BC}$)2=4:9,
∴$\frac{DE}{BC}$=$\frac{2}{3}$,
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{2}{3}$,
∴AD:BD=2:1.
点评 本题考查了相似三角形的判定,三角形面积的计算公式,相似三角形对应边比值相等的性质,本题中求得$\frac{AD}{AB}$=$\frac{2}{3}$是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
16.某校开展“节约每一滴水”活动,为了解开展活动的一个月以来节约用水的情况,从八年级的400名同学中选出20名同学统计了各自家庭一个月的节水情况,统计结果见下表:
请你估计这400名同学的家庭一个月节约用水的总量大约是130m3.
| 节水量/m3 | 0.2 | 0.25 | 0.3 | 0.4 | 0.5 |
| 家庭数/个 | 2 | 4 | 6 | 7 | 1 |
18.如图,函数y=-x(x<0)的图象是( )
| A. |  | B. |  | C. |  | D. |  |
8.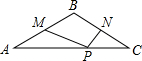 如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上的一个动点,M、N分别是AB、BC的中点,若PM+PN的最小值为2,则△ABC的周长是( )
如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上的一个动点,M、N分别是AB、BC的中点,若PM+PN的最小值为2,则△ABC的周长是( )
 如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上的一个动点,M、N分别是AB、BC的中点,若PM+PN的最小值为2,则△ABC的周长是( )
如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上的一个动点,M、N分别是AB、BC的中点,若PM+PN的最小值为2,则△ABC的周长是( )| A. | 2+$\sqrt{3}$ | B. | 4 | C. | 4+2$\sqrt{3}$ | D. | 12 |
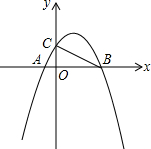 如图,二次函数y=-x2+ax+b的图象与x轴交于$A(-\frac{1}{2},0)$,B(2,0)两点,且与y轴交于点C.
如图,二次函数y=-x2+ax+b的图象与x轴交于$A(-\frac{1}{2},0)$,B(2,0)两点,且与y轴交于点C. 有理数a,b,c在数轴上所表示的点如图所示,请在空格处填上“<”或“>”:a×b-c>0.
有理数a,b,c在数轴上所表示的点如图所示,请在空格处填上“<”或“>”:a×b-c>0.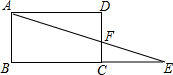 如图,点E是矩形ABCD的边BC延长线上的一点,AE交CD于F,若CF:DF=1:2,则△FCE与△ABE的面积的比是$\frac{1}{9}$.
如图,点E是矩形ABCD的边BC延长线上的一点,AE交CD于F,若CF:DF=1:2,则△FCE与△ABE的面积的比是$\frac{1}{9}$.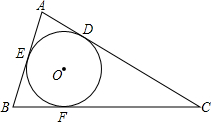 如图,已知⊙O为△ABC的内切圆,D、E、F为切点,P是异于E、F的⊙O上一动点,若∠A+∠C=130°,则∠EPF等于65°或115°.
如图,已知⊙O为△ABC的内切圆,D、E、F为切点,P是异于E、F的⊙O上一动点,若∠A+∠C=130°,则∠EPF等于65°或115°.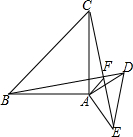 如图,AB=AC,AD=AE,∠BAC=∠DAE=90°.
如图,AB=AC,AD=AE,∠BAC=∠DAE=90°.