题目内容
14.解方程组:$\left\{\begin{array}{l}{4{x}^{2}-{y}^{2}=0}\\{3{x}^{2}-xy+x+2y+6=0}\end{array}\right.$.分析 由①得:2x-y=0,2x+y=0,这样原方程组化成两个二元二次方程组,求出每个方程组的解即可.
解答 解:$\left\{\begin{array}{l}{4{x}^{2}-{y}^{2}=0①}\\{3{x}^{2}-xy+x+2y+6=0②}\end{array}\right.$
由①得:2x-y=0,2x+y=0,
原方程组化为:①$\left\{\begin{array}{l}{2x-y=0}\\{3{x}^{2}-xy+x+2y+6=0}\end{array}\right.$,②$\left\{\begin{array}{l}{2x+y=0}\\{3{x}^{2}-xy+x+2y+6=0}\end{array}\right.$,
解方程组①得:$\left\{\begin{array}{l}{{x}_{1}=-2}\\{{y}_{1}=-4}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-3}\\{{y}_{2}=-6}\end{array}\right.$,方程组②无解,
所以原方程组的解为:$\left\{\begin{array}{l}{{x}_{1}=-2}\\{{y}_{1}=-4}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-3}\\{{y}_{2}=-6}\end{array}\right.$.
点评 本题考查了解高次方程组,能把高次方程组转化成二元二次方程组(降次)是解此题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
19.某小区开展“节约用水,从我做起”活动,下表是从该小区抽取的10个家庭,8月份比7月份节约用水情况统计:
那么这10个家庭8月份比7月份的节水量的平均数是( )
| 节水量(m3) | 0.2 | 0.3 | 0.4 | 0.5 |
| 家庭数(个) | 1 | 2 | 3 | 4 |
| A. | 0.5m3 | B. | 0.4m3 | C. | 0.35m3 | D. | 0.3m3 |
6.2016年,义乌市经济总体平稳,全年实现地区生产总值1118亿元.将1118亿元用科学记数法表示应为(单位:元)( )
| A. | 1.118×103 | B. | 1.118×1010 | C. | 1.118×1011 | D. | 1.118×1012 |
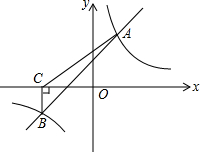 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4)、B(-4,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4)、B(-4,n)两点. 如图,在?ABCD中,AE=CG,求证:GF=HE.
如图,在?ABCD中,AE=CG,求证:GF=HE. 如图,E是?ABCD边DC上一点,请你只用一把没有刻度的直尺,在AB边上确定一点F,使得BF=DE,画出示意图,并简要说明画图过程.
如图,E是?ABCD边DC上一点,请你只用一把没有刻度的直尺,在AB边上确定一点F,使得BF=DE,画出示意图,并简要说明画图过程. 如图,在Rt△ABC中,∠C=90°,∠A=30°,D为AB中点,DE⊥AC于E,AB=8,则DE的长度为( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,D为AB中点,DE⊥AC于E,AB=8,则DE的长度为( )