题目内容
13.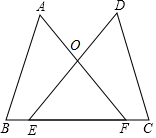 已知:如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
已知:如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.(1)求证:AB=DC;
(2)求证:△OEF是等腰三角形.
分析 (1)只要证明△ABF≌△DCE(AAS)即可;
(2)只要证明∠AFB=∠DEC即可;
解答 证明:(1)∵BE=CF,
∴BF=CE,
∵在△ABF和△DCE中
$\left\{\begin{array}{l}{∠A=∠D}\\{∠B=∠C}\\{BF=CE}\end{array}\right.$,
∴△ABF≌△DCE(AAS),
∴AB=DC;
(2)∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∴OE=OF,
∴△OEF是等腰三角形.
点评 本题考查全等三角形的判定和性质.等腰三角形的判定等知识,解题的关键是正确寻找全等三角形解决问题,属于基础题.

练习册系列答案
相关题目
 如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.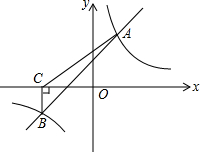 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4)、B(-4,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4)、B(-4,n)两点. 如图,E是?ABCD边DC上一点,请你只用一把没有刻度的直尺,在AB边上确定一点F,使得BF=DE,画出示意图,并简要说明画图过程.
如图,E是?ABCD边DC上一点,请你只用一把没有刻度的直尺,在AB边上确定一点F,使得BF=DE,画出示意图,并简要说明画图过程.