Question

17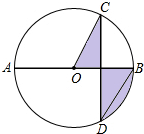．如图，AB是⊙O的直径，弦CD⊥AB，∠CDB=30°，CD=2$\sqrt{3}$，则阴影部分图形的面积为（　　）

• A． 4π
• B． 2π
• C． π
• D． $\frac{2π}{3}$

Answer 1

分析 根据垂径定理求得CE=ED=$\sqrt{3}$；然后由圆周角定理知∠COE=60°．然后通过解直角三角形求得线段OC，求出扇形COB面积，即可得出答案．

解答 解：∵AB是⊙O的直径，弦CD⊥AB，CD=2$\sqrt{3}$，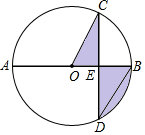

∴CE=$\frac{1}{2}$CD=$\sqrt{3}$，∠CEO=90°，
∵∠CDB=30°，
∴∠COB=2∠CDB=60°，
∴OC=$\frac{CE}{sin60°}$=2，
∴阴影部分的面积S=S_扇形COB=$\frac{60π×{2}^{2}}{360}$=$\frac{2π}{3}$，
故选D．

点评 本题考查了垂径定理、解直角三角形，圆周角定理，扇形面积的计算等知识点，能知道阴影部分的面积=扇形COB的面积是解此题的关键．