题目内容
2.不等式组$\left\{\begin{array}{l}{x<1}\\{x>m-1}\end{array}\right.$,若不等式组无解,则m的值可以为3(写出一个即可)若不等式组恰有两个整数解,则m的取值范围是-1≤m<0.分析 根据不等式组无解,可求m的值;根据不等式组的整数解个数,列出关于m的不等式组,解之得出m的范围,从而得出答案.
解答 解:∵不等式组$\left\{\begin{array}{l}{x<1}\\{x>m-1}\end{array}\right.$无解,
∴m-1≥1,
解得m≥2,
则m的值可以为3;
∵不等式组$\left\{\begin{array}{l}{x<1}\\{x>m-1}\end{array}\right.$恰有两个整数解,
∴该不等式组的整数解为0,-1,
则-2≤m-1<-1,
解得:-1≤m<0.
故答案为:3;-1≤m<0.
点评 本题考查的是不等式组的整数解和解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
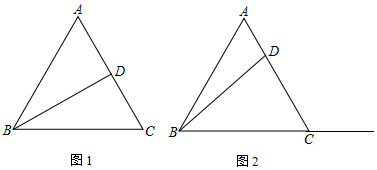
 如图,CE是△ABC的外角∠ACD的平分线,交BA的延长线于点E,若∠E=20°,∠B=30°,则∠BAC=70°.
如图,CE是△ABC的外角∠ACD的平分线,交BA的延长线于点E,若∠E=20°,∠B=30°,则∠BAC=70°.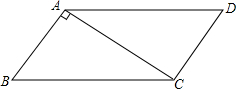 如图:在?ABCD中,CA⊥BA,AB=3,AC=4,求?ABCD的周长及面积.
如图:在?ABCD中,CA⊥BA,AB=3,AC=4,求?ABCD的周长及面积.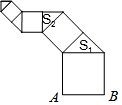 按如图所示的方式作正方形和等腰直角三角形,若第一个正方形的边AB=1,第1个等腰直角三角形面积为S1,第2个等腰直角三角形的面积为S2,…,第n个等腰直角三角形的面积为Sn(其中n为正整数),则Sn=$\frac{1}{{2}^{n+1}}$.
按如图所示的方式作正方形和等腰直角三角形,若第一个正方形的边AB=1,第1个等腰直角三角形面积为S1,第2个等腰直角三角形的面积为S2,…,第n个等腰直角三角形的面积为Sn(其中n为正整数),则Sn=$\frac{1}{{2}^{n+1}}$.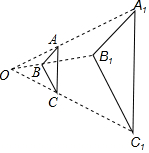 如图,△ABC与△A1B1C1是以点O为位似中心的位似图形,且位似比为1:3,若△A1B1C1面积为3,则△ABC的面积为$\frac{1}{3}$.
如图,△ABC与△A1B1C1是以点O为位似中心的位似图形,且位似比为1:3,若△A1B1C1面积为3,则△ABC的面积为$\frac{1}{3}$. 如图,△ABC的三个顶点均在格点上,且A(1,3),B(2,1)
如图,△ABC的三个顶点均在格点上,且A(1,3),B(2,1)