题目内容
13. 如图,点O是直线AB上一点,OC是∠AOD的平分线,已知∠AOC的补角是150°20′,则∠AOD的度数是59°20′.
如图,点O是直线AB上一点,OC是∠AOD的平分线,已知∠AOC的补角是150°20′,则∠AOD的度数是59°20′.
分析 先根据补角的定义求得∠AOC的度数,然后由角平分线的定义可知∠AOD=2∠AOC,从而可求得∠AOD的度数.
解答 解:∵∠AOC的补角是150°20′,
∴∠AOC=180°-150°20′=29°40′.
∵OC是∠AOD的平分线,
∴∠AOD=2∠AOC=2×29°40′=59°20′.
故答案为:59°20′.
点评 本题主要考查的是补角的定义、度分秒的换算、角平分线的定义,掌握相关知识是解题的关键.

练习册系列答案
相关题目
3.列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的$\frac{1}{2}$倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价-进价)
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
| 甲 | 乙 | |
| 进价(元/件) | 20 | 30 |
| 售价(元/件) | 29 | 40 |
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
1.某商店代销一批季节性服装,每套代销成本40元,第一个月每套销售定价为52元时,可售出180套;应市场变化需上调第一个月的销售价,预计销售定价每增加1元,销售量将减少10套.
(1)若设第二个月的销售定价每套增加x元,填写表格:
(2)若商店预计要在第二个月的销售中获利2000元,则第二个月销售定价每套多少元?
(3)若要使第二个月利润达到最大,应定价为多少?此时第二个月的最大利润是多少?
(1)若设第二个月的销售定价每套增加x元,填写表格:
| 时间 | 第一个月 | 第二个月 |
| 销售定价(元) | 52 | 52+x |
| 销售量(套) | 180 | 180-10x |
(3)若要使第二个月利润达到最大,应定价为多少?此时第二个月的最大利润是多少?
3.某旅游景点的门票价格如下表:
某校八年级(1)、(2)两班共100多人计划去游览该景点,其中(1)班人数少于50人,(2)班人数有50多人,如果两班都以班为单位单独购票,则一共支付7965元;如果两班联合起来作为一个团体购票,则只需花费7210元.两个班各有多少名学生?
| 购票人数/人 | 1-50 | 51-100 | 100以上 |
| 每人门票价/元 | 80 | 75 | 70 |
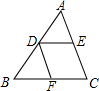 如图,在△ABC中,D为AB的中点,DE∥BC,交AC于点E,DF∥AC,交BC于点F.
如图,在△ABC中,D为AB的中点,DE∥BC,交AC于点E,DF∥AC,交BC于点F. 已知一次函数y1=-2x-3与y2=$\frac{1}{2}$x+2.
已知一次函数y1=-2x-3与y2=$\frac{1}{2}$x+2.