题目内容
8. 已知一次函数y1=-2x-3与y2=$\frac{1}{2}$x+2.
已知一次函数y1=-2x-3与y2=$\frac{1}{2}$x+2.(1)在同一平面直角坐标系中,画出这两个函数的图象;
(2)根据图象,不等式-2x-3>$\frac{1}{2}$x+2的解集为x<-2;
(3)求两图象和y轴围成的三角形的面积.
分析 (1)先求出直线y1=-2x-3,y2=$\frac{1}{2}$x+2与x轴和y轴的交点,再画出两函数图象即可;
(2)直线y1=-2x-3的图象落在直线y2=$\frac{1}{2}$x+2上方的部分对应的x的取值范围就是不等式-2x-3>$\frac{1}{2}$x+2的解集;
(3)根据三角形的面积公式求解即可.
解答 解:(1)函数y1=-2x-3与x轴和y轴的交点分别是(-1.5,0)和(0,-3),
y2=$\frac{1}{2}$x+2与x轴和y轴的交点分别是(-4,0)和(0,2),
其图象如图: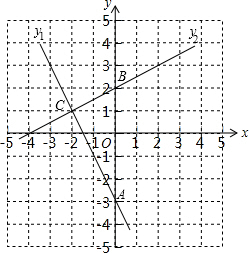
(2)观察图象可知,函数y1=-2x-3与y2=$\frac{1}{2}$x+2交于点(-2,1),
当x<-2时,直线y1=-2x-3的图象落在直线y2=$\frac{1}{2}$x+2的上方,即-2x-3>$\frac{1}{2}$x+2,
所以不等式-2x-3>$\frac{1}{2}$x+2的解集为x<-2;
故答案为x<-2;
(3)∵y1=-2x-3与y2=$\frac{1}{2}$x+2与y轴分别交于点A(0,-3),B(0,2),
∴AB=5,
∵y1=-2x-3与y2=$\frac{1}{2}$x+2交于点C(-2,1),
∴△ABC的边AB上的高为2,
∴S△ABC=$\frac{1}{2}$×5×2=5.
点评 本题考查的是一次函数与一元一次不等式,一次函数的图象,三角形的面积,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
18. 如图,在边长为9cm的等边三角形ABC中,D为BC上一点,且BD=3cm,E在AC上,∠ADE=60°,则AE的长为( )
如图,在边长为9cm的等边三角形ABC中,D为BC上一点,且BD=3cm,E在AC上,∠ADE=60°,则AE的长为( )
 如图,在边长为9cm的等边三角形ABC中,D为BC上一点,且BD=3cm,E在AC上,∠ADE=60°,则AE的长为( )
如图,在边长为9cm的等边三角形ABC中,D为BC上一点,且BD=3cm,E在AC上,∠ADE=60°,则AE的长为( )| A. | 2cm | B. | 5cm | C. | 6cm | D. | 7cm |
17.元旦期间,某玩具店从玩具批发市场批发玩具进行零售,部分玩具批发价格与零售价格如下表:
请解答下列问题:
(1)第一天,该玩具店批发A,B两种型号玩具共59个,用去了1344元钱,这两种型号玩具当天全部售完后一共能赚多少元钱?
(2)第二天,该玩具店用第一天全部售完后的总零售价钱批发A,B,C三种型号玩具中的两种玩具共68个,且当天全部售完,请通过计算说明该玩具店第二天应如何进货才能使全部售完后赚的钱最多?
| 玩具型号 | A | B | C |
| 批发价(元/个) | 20 | 24 | 28 |
| 零售价(元/个) | 25 | 30 | 40 |
(1)第一天,该玩具店批发A,B两种型号玩具共59个,用去了1344元钱,这两种型号玩具当天全部售完后一共能赚多少元钱?
(2)第二天,该玩具店用第一天全部售完后的总零售价钱批发A,B,C三种型号玩具中的两种玩具共68个,且当天全部售完,请通过计算说明该玩具店第二天应如何进货才能使全部售完后赚的钱最多?
18.下列命题中是真命题的是( )
| A. | 算术平方根等于自身的数只有1 | |
| B. | $\sqrt{\frac{1}{2}}$是最简二次根式 | |
| C. | 有一个角等于60°的三角形是等边三角形 | |
| D. | 两角及其夹边分别相等的两个三角形全等 |


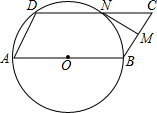 如图,平行四边形ABCD中,AB=2,∠A=60°,以AB为直径的⊙O过点D,点M是BC边上一点(点M不与B,C重合),过点M作BC的垂线MN,交CD边于点N.
如图,平行四边形ABCD中,AB=2,∠A=60°,以AB为直径的⊙O过点D,点M是BC边上一点(点M不与B,C重合),过点M作BC的垂线MN,交CD边于点N. 如图,点O是直线AB上一点,OC是∠AOD的平分线,已知∠AOC的补角是150°20′,则∠AOD的度数是59°20′.
如图,点O是直线AB上一点,OC是∠AOD的平分线,已知∠AOC的补角是150°20′,则∠AOD的度数是59°20′.