题目内容
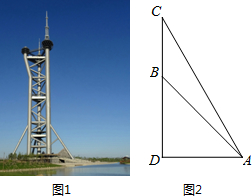
2. 已知:如图,在?ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.求证:△DOE≌△BOF.
已知:如图,在?ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.求证:△DOE≌△BOF.
分析 由平行四边形的性质得出BO=DO,AD∥BC,证出∠EDO=∠FBO,由ASA证明△DOE≌△BOF即可.
解答 证明:∵在□ABCD中,O为对角线BD的中点,
∴BO=DO,AD∥BC,
∴∠EDO=∠FBO,
在△EOD和△FOB中,
$\left\{\begin{array}{l}{∠EDO=∠FBO}&{\;}\\{DO=BO}&{\;}\\{∠DOE=∠BOF}&{\;}\end{array}\right.$,
∴△DOE≌△BOF(ASA).
点评 此题主要考查了平行四边形的性质以及全等三角形的判定;熟练掌握平行四边形的性质是解决问题的关键.

练习册系列答案
相关题目
12.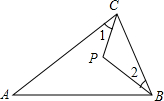 如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )
如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )
 如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )
如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )| A. | 110° | B. | 120° | C. | 130° | D. | 140° |
7.已知关于x的一元二次方程x2+$\sqrt{k-1}$x-1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k>-7 | B. | k≥-7 | C. | k≥0 | D. | k≥1 |