题目内容
3.计算;(1)($\frac{1}{3}$-$\frac{1}{5}$)•($\frac{1}{5}$)-2÷|-$\frac{1}{3}$|+(1-$\sqrt{3}$)0+(-0.25)2007•42008
(2)(3-1m3n-2)-2•(m-2n)-3
(3)$\frac{(2a{b}^{2})^{-2}•({a}^{2}{b)}^{2}}{(3{a}^{3}{b}^{2})•(a{b}^{3})^{-2}}$
(4)$\frac{[4(x-y)^{2}(x+y)^{-2}]^{2}}{[2(x+y)^{-1}(x-y)]^{-2}}$.
分析 (1)根据负整数指数幂,即可解答;
(2)根据负整数指数幂,即可解答;
(3)根据负整数指数幂,即可解答;
(4)根据负整数指数幂,即可解答.
解答 解:(1)原式=$(\frac{5}{15}-\frac{3}{15})×25÷\frac{1}{3}+1+(-0.25×4)^{2007}×4$
=$\frac{2}{15}×25×3+1+(-4)$
=10+1-4
=7.
(2)原式=32m-6n4•m6n-3
=9n.
(3)原式=$\frac{{2}^{-2}{a}^{-2}{b}^{-4}•{a}^{4}{b}^{2}}{3{a}^{3}{b}^{2}•{a}^{-2}{b}^{-6}}$
=$\frac{\frac{1}{4}{a}^{2}{b}^{-2}}{3a{b}^{-4}}$
=$\frac{a{b}^{2}}{12}$.
(4)原式=$\frac{16(x-y)^{4}(x+y)^{-4}}{\frac{1}{4}(x+y)^{2}(x-y)^{-2}}$
=$\frac{64(x-y)^{6}}{(x+y)^{6}}$.
点评 本题考查了负整数指数幂,解决本题的关键是熟记负整数指数幂.

练习册系列答案
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
14.在下列长度的四根木棒中,能与4cm、9cm长的两根木棒钉成一个三角形的是( )
| A. | 13cm | B. | 6cm | C. | 5cm | D. | 4cm |
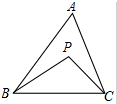 如图,在△ABC中,∠ABP=2∠PBC,∠ACP=2∠PCB.
如图,在△ABC中,∠ABP=2∠PBC,∠ACP=2∠PCB. 随着房价的上涨,某开房商调研发现大多数人无力购买面积较大的房子,该开发商决定建造一批“经济适用房”.如图是一套小户型“经济适用房”的平面尺寸图.
随着房价的上涨,某开房商调研发现大多数人无力购买面积较大的房子,该开发商决定建造一批“经济适用房”.如图是一套小户型“经济适用房”的平面尺寸图. 如图:在△ABC中,AB=AC=$\sqrt{5}$,BC=4,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为1.
如图:在△ABC中,AB=AC=$\sqrt{5}$,BC=4,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为1.